Sie heissen auch trochoidale Schwerewellen (curtate cycloids).
Eine Trochoide entsteht als Superposition einer gleichmässigen Kreisbewegung und einer Bewegung mit konstanter Geschwindigkeit parallel zur Kreisebene.
| Schwerewellen über tiefem Wasser haben ungefähr die Form einer verkürzten Zykloiden; man bezeichnet sie auch als trochoidale Wasserwellen. Die Wellenfunktion kann mit folgender Beobachtung begründet werden: Läuft die Welle an einer Stelle vorbei, so bewegt sich ein Element der Oberfläche näherungsweise auf einem vertikalen Kreis. Die Kreisebene ist parallel zur Ausbreitungsrichtung der Welle. Fährt ein Boot neben der Welle her, so bewegt sich dasselbe Oberflächenelement relativ zum Boot auf einer Trochoiden. In dieser Darstellung tritt kein Massetransport auf, d.h. die Oberflächenelemente bleiben im Mittel an Ort (Franz Josef von Gerstner, 1804) Eine Trochoide (gr. trochos: Rad) wird z.B. von einem Reflektor an einer Fahrradspeiche beschrieben, wenn das Fahrrad gleichmässig geradeaus fährt. Zykloiden entstehen als Überlagerung von einer gleichmässigen Kreisbewegung und einer gleichmässig geradlinigen Rollbewegung. Bei verkürzten Zykloiden liegt der betrachtete Punkt im Inneren der rollenden Kreisscheibe, bei einer gewöhnlichen oder gespitzten Zykloiden auf der Kreislinie und bei einer verlängerten Zyloiden in der Verlängerung des Kreisradius ausserhalb. Verlängerte Zykloiden haben Schlaufen, was bei Wellenbewegungen nicht auftritt. |
| Wasserwellen über tiefem Wasser sind näherungsweise verkürzte Zykloiden. Sie heissen auch trochoidale Schwerewellen (curtate cycloids). Eine Trochoide entsteht als Superposition einer gleichmässigen Kreisbewegung und einer Bewegung mit konstanter Geschwindigkeit parallel zur Kreisebene. |
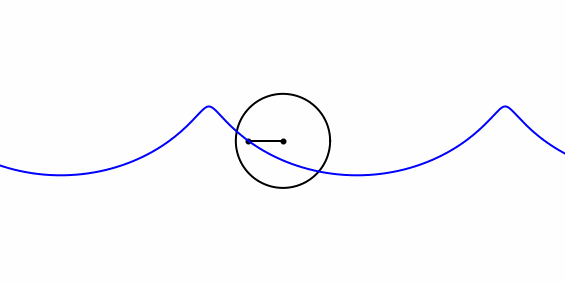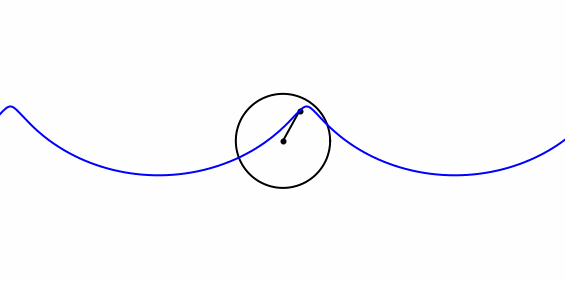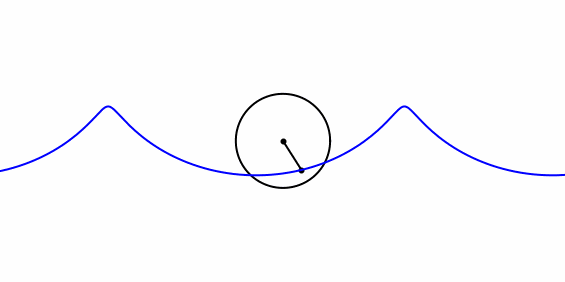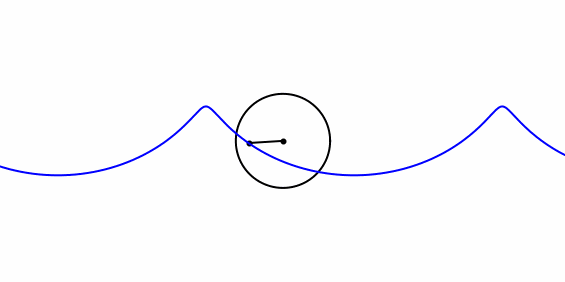 |
| Ein Punkt im Innern einer Kreisscheibe dreht sich gleichmässig um das ruhende Kreiszentrum. In einem Bezugsystem, wo sich das Kreiszentrum gleichmässig geradlinig bewegt, bewegt sich derselbe Punkt entlang einer verkürzten Zykloide oder Trochoide. (animated gif aus 100 Einzelbildern, berechnet mit Python) |