Tropfendes Pendel

Welche Bahnen beschreiben idealisierte Wassertropfen, die sich von einem idealisierten Stangenpendel lösen? Das Pendel wird als mathematisches Pendel modelliert, die Wassertropfen als Massenpunkte, die sich tangential zur Pendelbahn vom Pendel lösen. Die Wassertropfen haben bei der Ablösung dieselbe vektorielle Geschwindigkeit und Position wie die Pendelmasse. Die Bahnen der Tropfen sind Scharen von Wurfparabeln.

Parametrisierung: Das Pendel startet im tiefsten Punkt mit der Bahngeschwindigkeit
v_unten = (fgr)^1/2
Dabei ist r die Pendellänge, g die Fallbeschleunigung und f ein Faktor, der die Schwingungsdauer festlegt. Das Pendel steigt bis zur Höhe h = fr/2 über den tiefsten Punkt, d.h. ab f = 4 kann es einen vollständigen Kreis beschreiben.

Faktor f	Steighöhe	Amplitude
0	0	0
1	0.5 r	π/3 = 60°
2	1.0 r	π/2 = 90°
3	1.5 r	2π/3 = 120°
4	2.0 r	π = 180°
f	fr/2	π/2 + arcsin(f/2-1)

Tabelle 1: Steighöhe und Amplitude des Pendels als Funktion des Parameters f.
Im tiefsten Punkt ist v = √(fgr). Ab f = 4 kann das Pendel rotieren.

Nun folgen einige Bilder, welche die Bahnscharen zeigen. Der Winkelbereich zwischen den Extremalausschlägen wurde in ungefähr gleich grosse Winkelschritte unterteilt.

Abbildung 1: f = 1
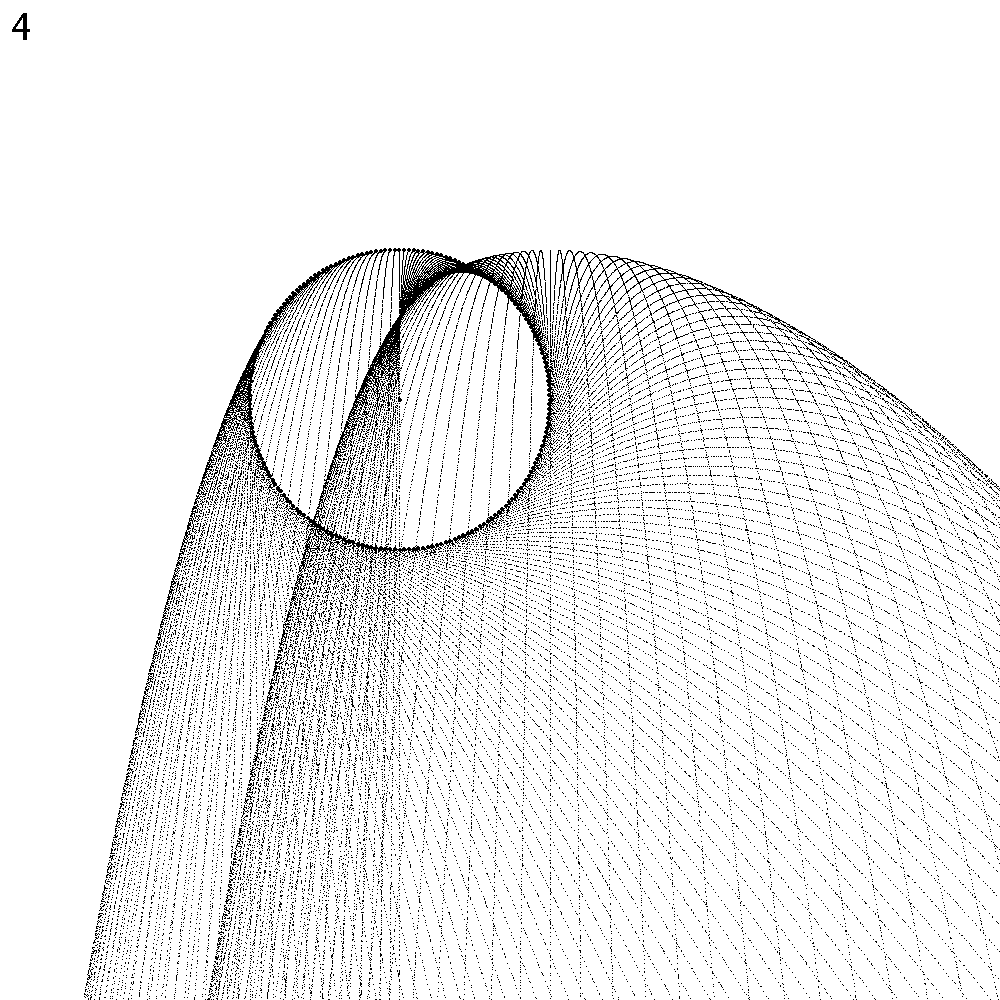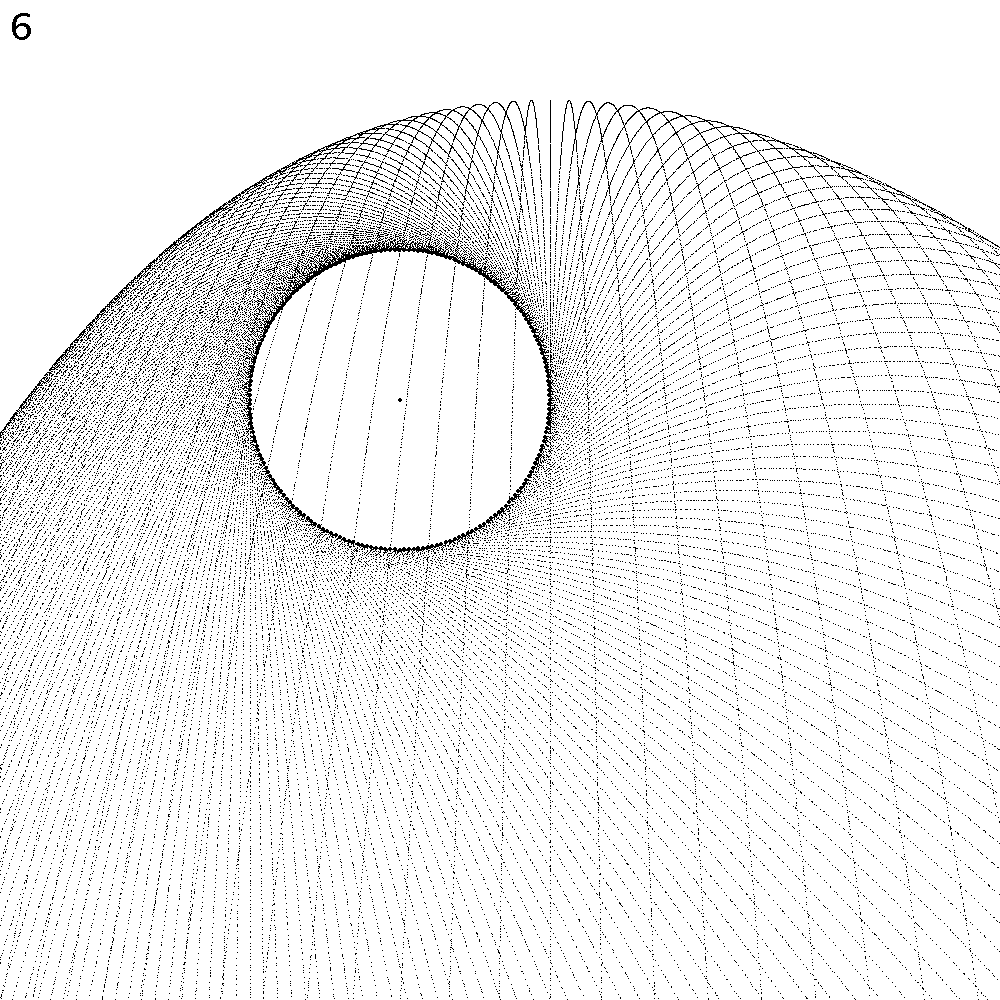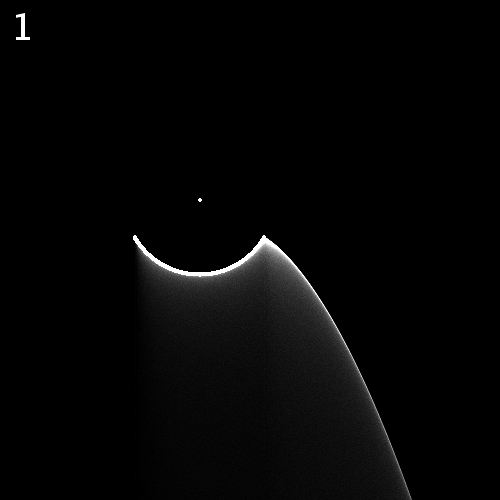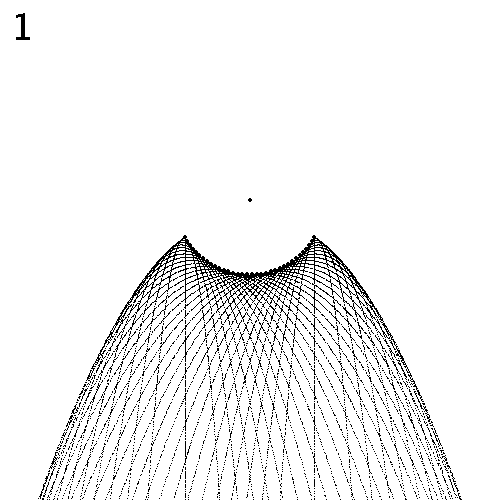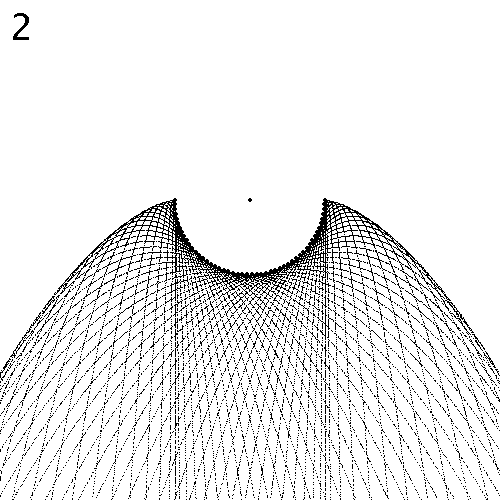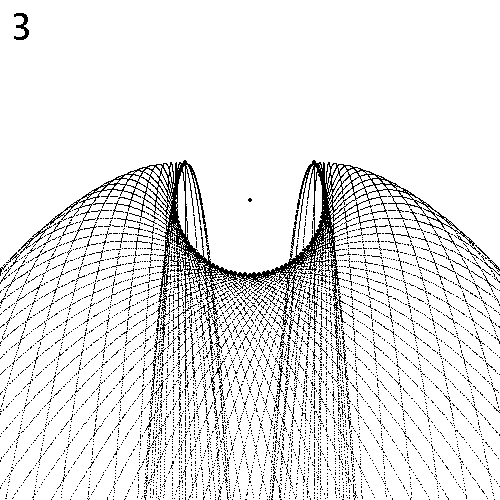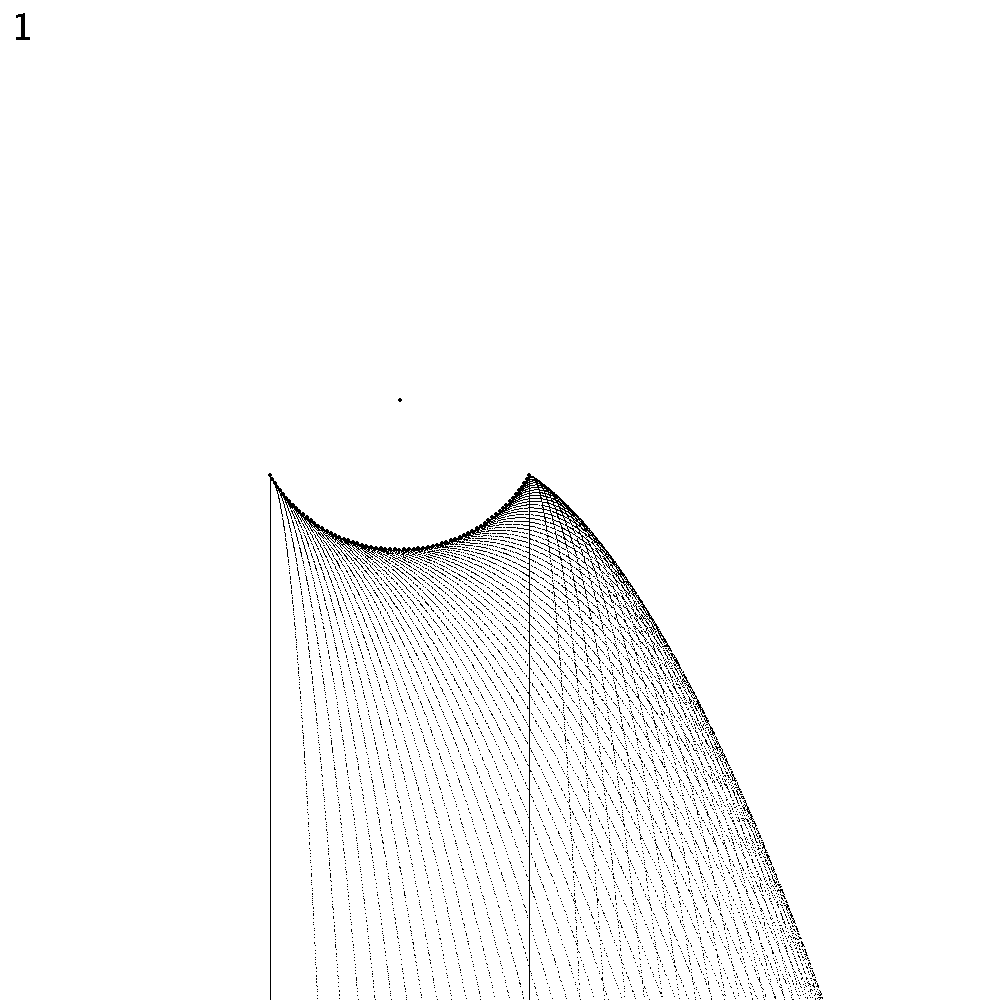
Das Pendel schwingt normal. Dargestellt ist jeweils eine Halbschwingung; die zweite Hälfte ergäbe ein spiegelsymmetrisches Bild. Die Zahl oben links im Bild ist der Faktor f. Der fette Punkt in der Mitte ist die Pendel-Aufhängung. Jene Stellen, wo sich Tropfen ablösen, sind ebenfalls mit einem fetten Punkt markiert.

Abbildung 2: f = 2
Das Pendel schwingt bis zur Horizontalen durch den Aufhängepunkt.

Abbildung 3: f = 3
Das Pendel schwingt über die Horizontale hinaus. Jene Tropfen, die sich zwischen der Horizontalen und dem Umkehrpunkt lösen, fallen deshalb in den Kreis hinein.

Abbildung 4: Kriechlösung f = 4
Das mathematische Pendel erreicht die Vertikale über der Aufhängung mit Geschwindigkeit Null nach unendlich langer Zeit. Ein Fadenpendel würde natürlich schon vorher in den Kreis hinein fallen.

Abbildung 5: f = 5
Das Pendel erreicht den höchsten Punkt mit Geschwindigkeit v = √(gr). Bei dieser Grenzgeschwindigkeit könnte ein Fadenpendel gerade einen vollständigen Kreis beschreiben. Die Wurfparabel, die im obersten Punkt des Kreises startet, hat dieselbe Krümmung wie der Kreis.

Abbildung 6: f = 6
Der Faden eines Fadenpendels wäre immer gespannt.

Abbildung 7: In diesen Bildern wurde die Dichte der Wurfparabeln der Tropfen durch Grauwerte codiert. Der Parameter f nimmt die Werte 1 bis 6 an.

Animation (5.7 Megabyte)

Animation 1: Was passiert mit den Kurvenscharen, wenn der Parameter f langsam erhöht wird? In dieser Animation variiert f von 0 bis 7 in Schritten von 0.1. Die Dichte der Kurven ist als Grauwert codiert.

Schliesslich folgen noch ein paar Bilder, wo die ganze Schwingung dargestellt ist, nicht nur eine Halbschwingung.

Abbildung 8: Symmetrisierte Darstellung der Wurfparabel-Scharen. Beide Halbschwingungen sind dargestellt. Der Parameter f nimmt die Werte 1 bis 6 an.

erste Version: 28. Juli 2008, letzte Änderung: 28. Juli 2008 / Martin Lieberherr

Zum Seitenanfang