Geladener Stab

Die Aufgabe, eine Probeladung zwischen zwei Punktladungen so zu positionieren, dass sie im Gleichgewicht ist, wird von uns allen im Unterricht verwendet. Aber wie sieht es aus, wenn man mehr Ladungen platzieren möchte? Wie verteilen sich die Ladungen auf einem dünnen Stab? In der folgenden Simulation wurden frei bewegliche Punktladungen gleicher Stärke und gleichen Vorzeichens auf einer Strecke endlicher Länge verteilt. Die Punktladungen können sich unter dem Einfluss der wechselseitigen Coulombkräfte frei bewegen. Nach einer gewissen Zeit stellt sich ein Gleichgewichtszustand ein.

Abb. 1: Durch numerische Simulation bestimmte Gleichgewichtslage von vier gleichen Punktladungen auf einem Stab.

In Abbildung 1 sieht man, dass die vier Punktladungen im Gleichgewicht zwar symmetrisch aber nicht gleichmässig verteilt sind. Die Ladungen drängen etwas gegen die Enden des Stabes. Diesen Fall kann man noch mit mässigem Aufwand rechnerisch behandeln. Die Gleichgewichtsbedingung für die 2. Ladung lautet:

Dabei ist d die Stablänge und q die Ladung eines Punktes. Die Gleichung lässt sich numerisch nach der Position x der Ladung lösen:
x/d = 0.31926..
Man kann das auch so in Abbildung 1 nachmessen. Der Abstand der äusseren Ladungen ist gleich der Stablänge.

Abb. 2: Gleichgewichtslage von 40 gleichen Punktladungen (fette Punkte unten) auf einem Stab. Nach oben abgetragen ist der Abstand zum rechten Nachbarpunkt (willkürliche Einheiten).

Abbildung 2 zeigt, dass die Abstände zwischen den Punktladungen gegen die Enden der Linie abnehmen, d.h. die Ladungsdichte ist an den Enden höher als in der Mitte. Das muss auch so sein, sonst kann kein Gleichgewicht herrschen.

Abb. 3: Wie Abbildung 2, aber mit 80 gleichen Punktladungen. Die Ladungen waren zu Beginn der Iteration gleichmässig verteilt.

Abb. 4: Wie Abbildung 2, aber mit 160 gleichen Punktladungen, die anfangs ungleichmässig verteilt waren (gegen die Enden konzentriert). Der simulierte Gleichgewichts-Endzustand hängt nicht von der Startverteilung ab.

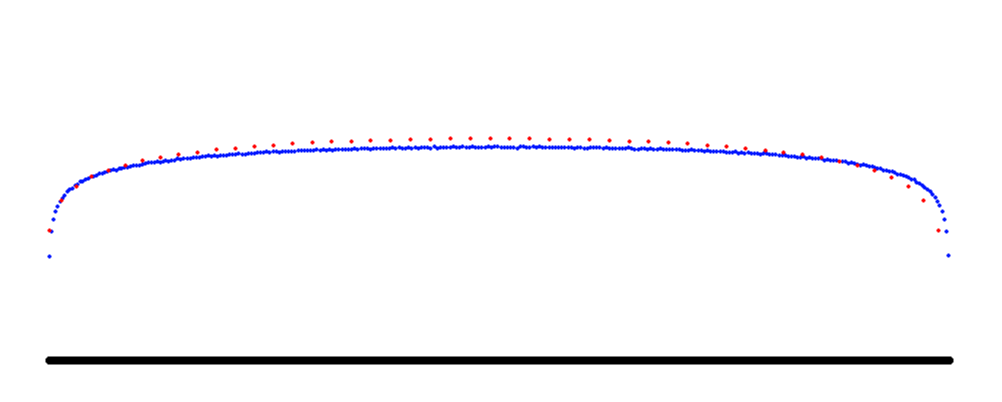Abb. 5: Wie Abbildung 2, aber mit 50 gleichen Punktladungen (rot) sowie 300 Ladungen (blau). Man kann erkennen, dass die Verteilung mit wachsender Zahl homogener wird.

Durch Zufall bin ich via [1] auf einen Artikel von J.D. Jackson [2] gestossen. Dort wird bewiesen, dass sich die - kontinuierlich gedachte - Ladung gleichmässig verteilt, wenn man den Radius eines geraden Drahtes gegen Null gehen lässt. Die Konvergenz ist allerdings sehr langsam ("logarithmisch") und hängt von den Details der Modellierung ab. Das Paradox, dass an den Enden eine erhöhte Ladungsdichte vorhanden sein müsste, damit sich ein Kräftegleichgewicht einstellt, löst sich ebenfalls auf. Salopp gesagt spielen im Grenzfall unendlich grosser Feldstärken kleinere Abweichungen keine Rolle mehr.

[1] M.H. Partovi "Eqilibrium charge density on an thin curved wire"
(Am. J. Phys. 77 (12), December 2009, p. 1173-1182)
[2] J.D. Jackson "Charge density on thin straight wire, revisited"
(Am. J. Phys. 68 (9) September 2000, p. 789-799)

15. Februar 2010 / M. Lieberherr

Zum Seitenanfang