Strahlenoptisch simulierte Regenbogenstreuung
In der folgenden Simulation kommen Lichtstrahlen von links und treffen auf eine perfekte Kugel (Wassertropfen). Der Tropfen hat Brechungsindex n relativ zur umgebenden Luft. Die Strahlen werden nach den Gesetzen der geometrischen Optik teilweise reflektiert und teilweise transmittiert.
Die Strahlen werden auf einer zufällig gewählten Höhe gestartet. An der Grenzfläche Luft-Wasser wird zufällig entweder reflektiert oder transmittiert mit einer Wahrscheinlichkeit, die dem Reflexionskoeffizienten (für s-polarisiertes Licht) entspricht. Die Helligkeit des Bildes entspricht der Dichte der Strahlen. Die Simulation ist zweidimensional, d.h. die Helligkeit entspricht eigentlich eher der Streuung an einem Stab als an einer Kugel. Für ein Bild wurden zwischen zehntausend und einer Million Strahlengänge gerechnet.

Damit das Bild übersichtlicher wird, werden in der folgenden Animation sukzessive jene Strahlabschnitte, die nicht zu einem Regenbogen beitragen, weggelassen:
Regenbogen_Streulicht.gif (944 kByte)
Folgende Animation zeigt den Effekt, wenn man mehr Strahlen für die Simulation verwendet:
Regenbogen_Belichtung.gif (880 kByte)
Folgende Animation demonstriert die Dispersion: Für jede Farbe hat Wasser einen anderen Brechungsindex. In der Simulation n = 1.340 für blau, 1.335 für grün und 1.330 für rot. Man sieht, dass sich der Regenbogen-Streuwinkel leicht verändert.
Regenbogen_farbig.gif (484 kByte)
Folgendes Standbild zeigt nochmals die Regenbogenstreuung. Das Bild ist mit einem Hochpassfilter traktiert worden, um die Feinstruktur sichtbar zu machen. Über- und unterbelichtete Stellen werden in der Helligkeit angeglichen, Kanten verstärkt. Für das Bild wurden 1 Million Strahlen losgeschickt. Der relative Brechungsindex des Tropfens ist n = 1.333.

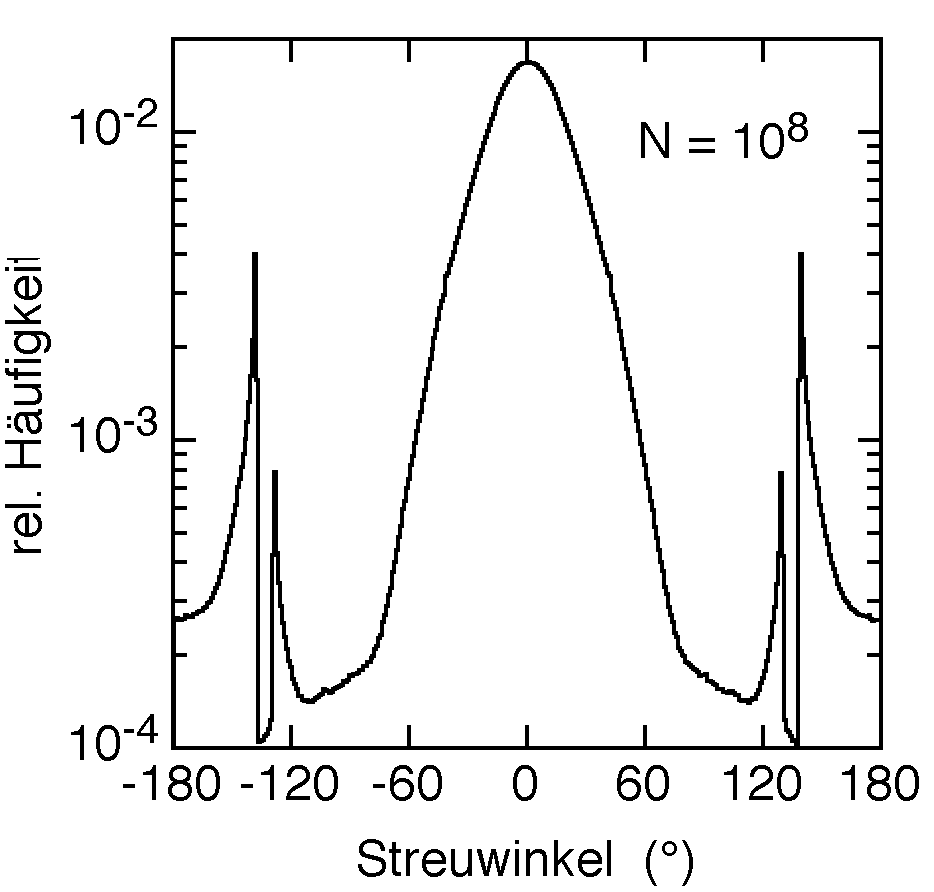
Können Sie den Zusammenhang mit folgender Darstellung sehen? Für das Histogramm wurden 100 Millionen Strahlen "abgeschossen". Der relative Brechungsindex der Kugel ist 1.333 wie oben.
Die nächsten zwei Bilder sind aus drei Farben (rot-grün-blau) kombiniert.

Das Bild oben wurde mit einem Hochpassfilter behandelt und unten dargestellt. Zusätzlich wurden noch die Farben verstärkt.

Der Hauptregenbogen entsteht, wenn Licht um ca. ±138 Grad rückwärts gestreut wird, bei einem leicht kleineren Winkel (129 Grad) sieht man den Nebenregenbogen, dazwischen den Alexander'schen Dunkelraum (nach Alexander von Aphrodisias, um 300 n.Chr.). Innerhalb des Hauptregenbogens (Streuwinkel über 138 Grad) ist es relativ hell, ebenso ausserhalb des Nebenregenbogens (unterhalb 129 Grad).
Die Ablenkwinkel lassen sich mit folgender Formel berechnen:
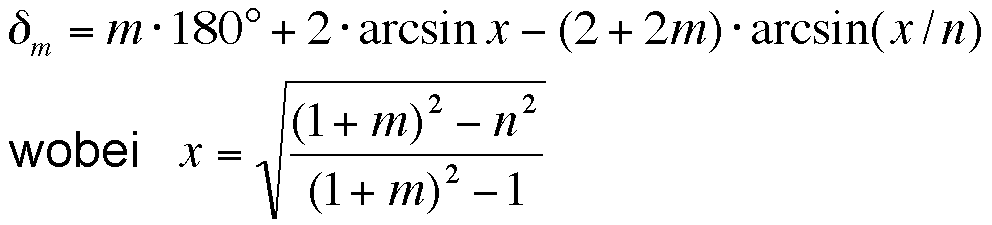
Die Variable x stellt den sog. relativen Stossparameter dar, die Variable m ist die Anzahl interner Reflexionen und n ist der relative Brechungsindex des Tropfens. Für n = 1.333 (wie in den letzten zwei Bildern) erhält man folgende Regenbogenwinkel:
| m |
Streuwinkel |
Bemerkungen |
| 1 |
137.92° |
Hauptregenbogen |
| 2 |
230.89° |
-129.11° Nebenregenbogen |
| 3 |
318.26° |
-41.74° |
| 4 |
403.70° |
43.70° |
| 5 |
488.23° |
128.23° |
Diese zweidimensionale, geometrisch-optische Simulation ist nur ein erster Schritt. Eine vertiefte Betrachtung kommt nicht um die räumliche Kugelgestalt und um den Wellencharakter des Lichts herum. Tropfen sind selten perfekt rund. Unsere Augen sind auch keine idealen Lichtempfänger, sie können z.B. von der Sonne oder einem hellen Hintergrund geblendet werden. Ausserdem hat die Sonne eine gewissen Ausdehnung; das Licht kommt also nicht exakt parallel an.
Ergänzungen: 30. April 2006, 1. Juni 2009 / Martin Lieberherr