
 |
 |
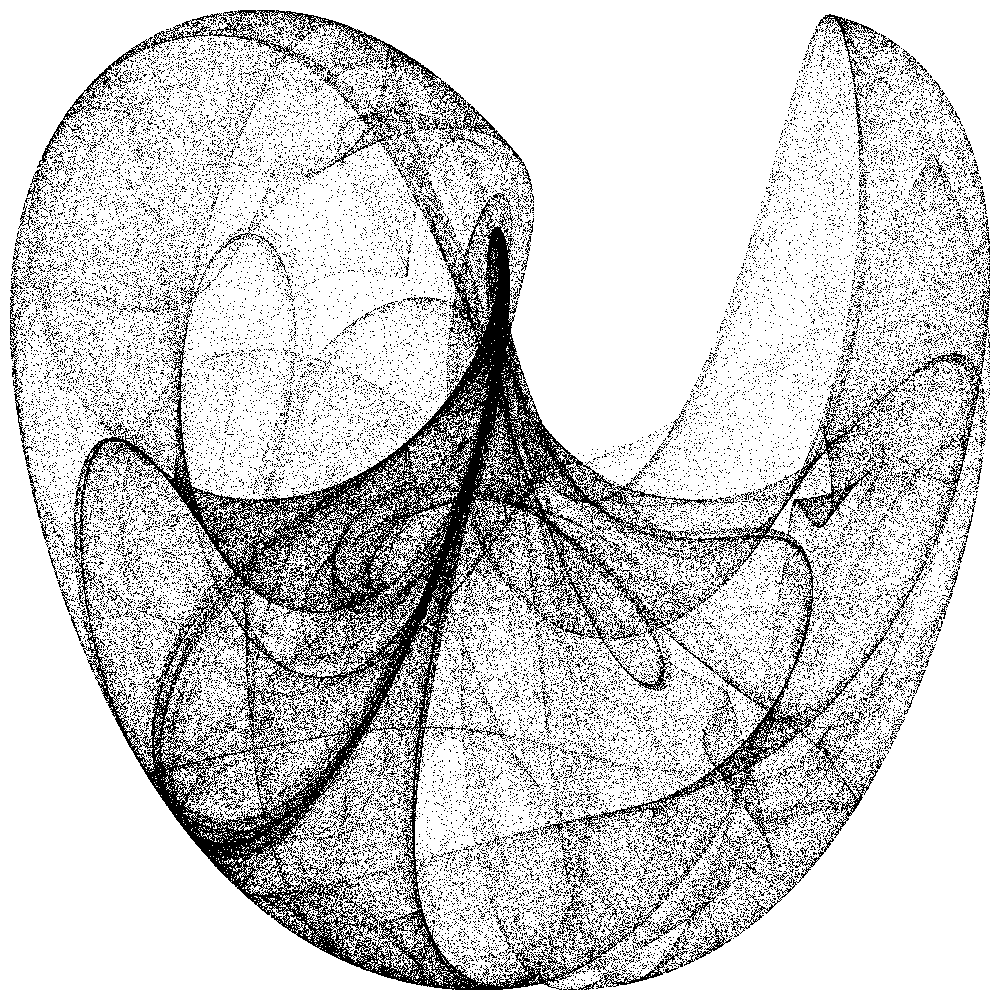
| Abb. 1a: a=1.419, b=-2.284, c=2.427, d=2.177 | Abb. 1b: a=1.419, b=-2.284, c=2.427, d=2.177 |
 |
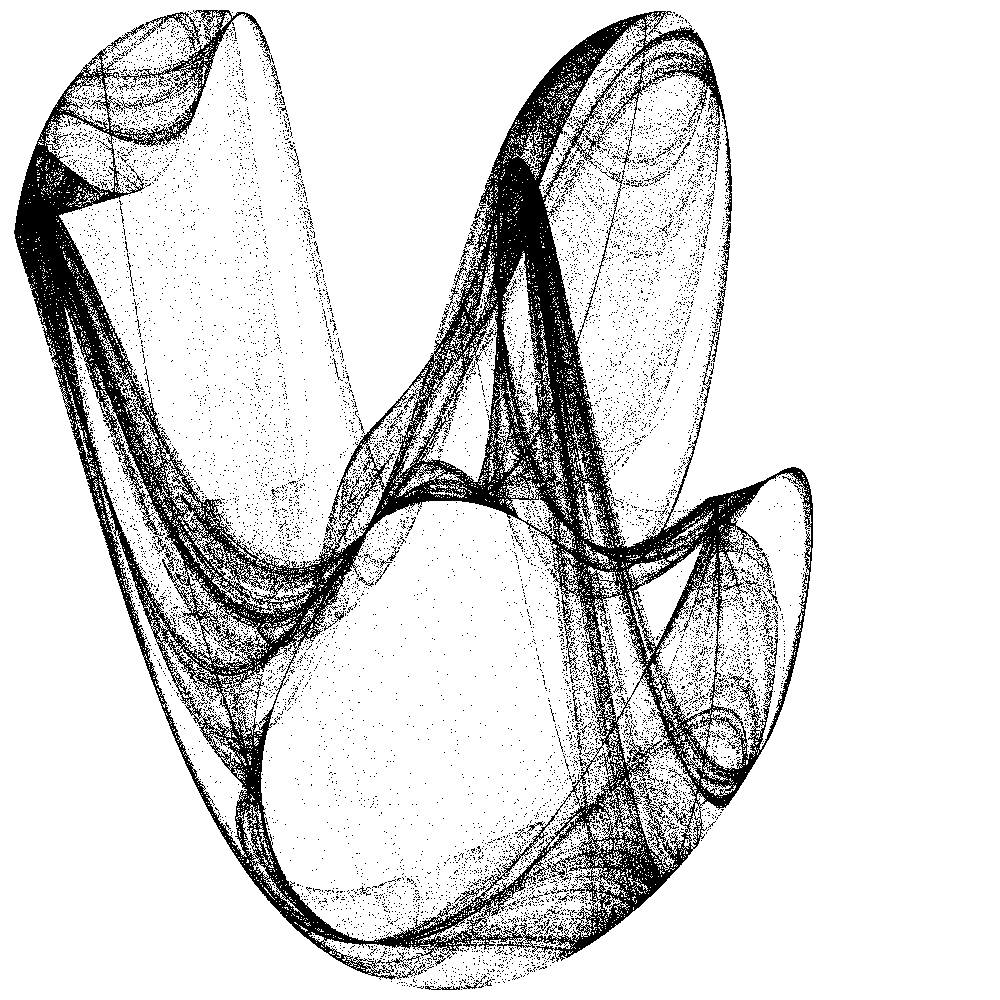 |
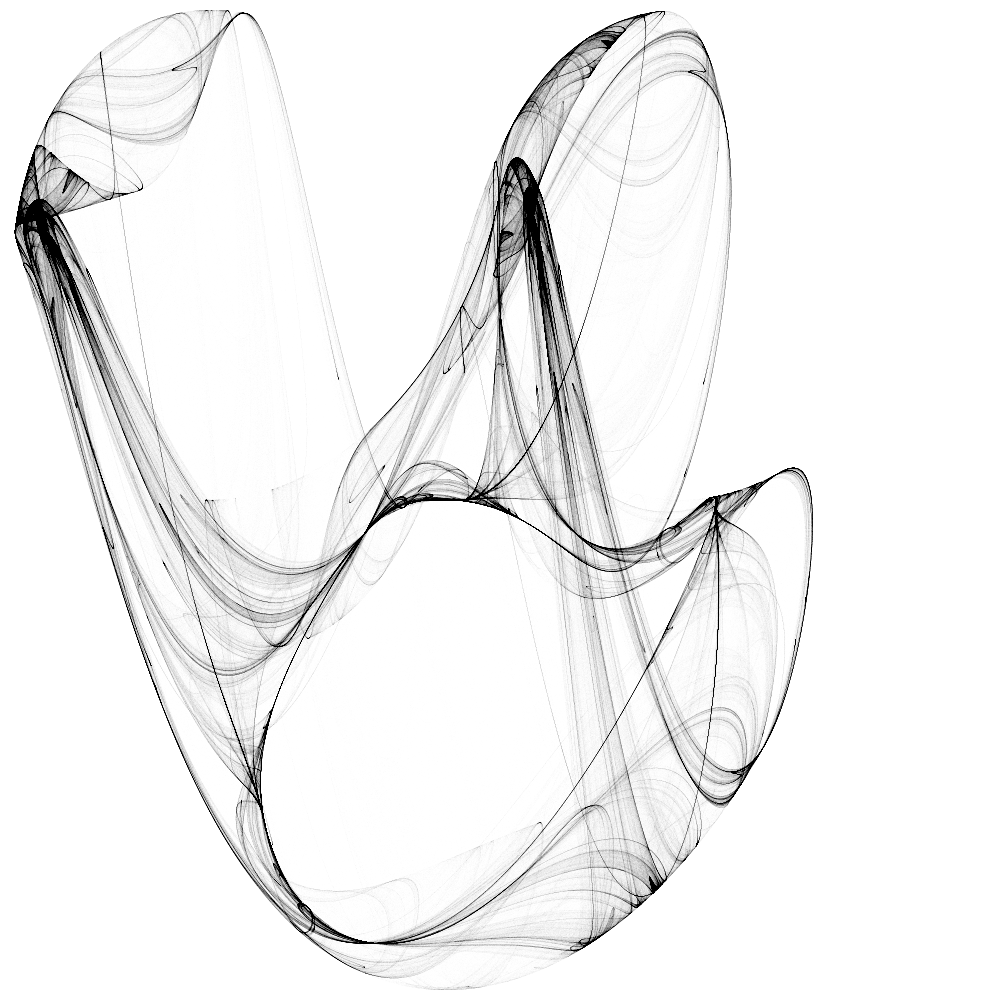
| Abb. 2a: a=-0.895, b=1.590, c=1.851, d=2.197 | Abb. 2b: a=-0.895, b=1.590, c=1.851, d=2.197 |
 |
 |
| Abb. 3a: a=2.033, b=-0.789, c=-0.596, d=-1.782 | Abb. 3b: a=2.033, b=-0.789, c=-0.596, d=-1.782 |
 |
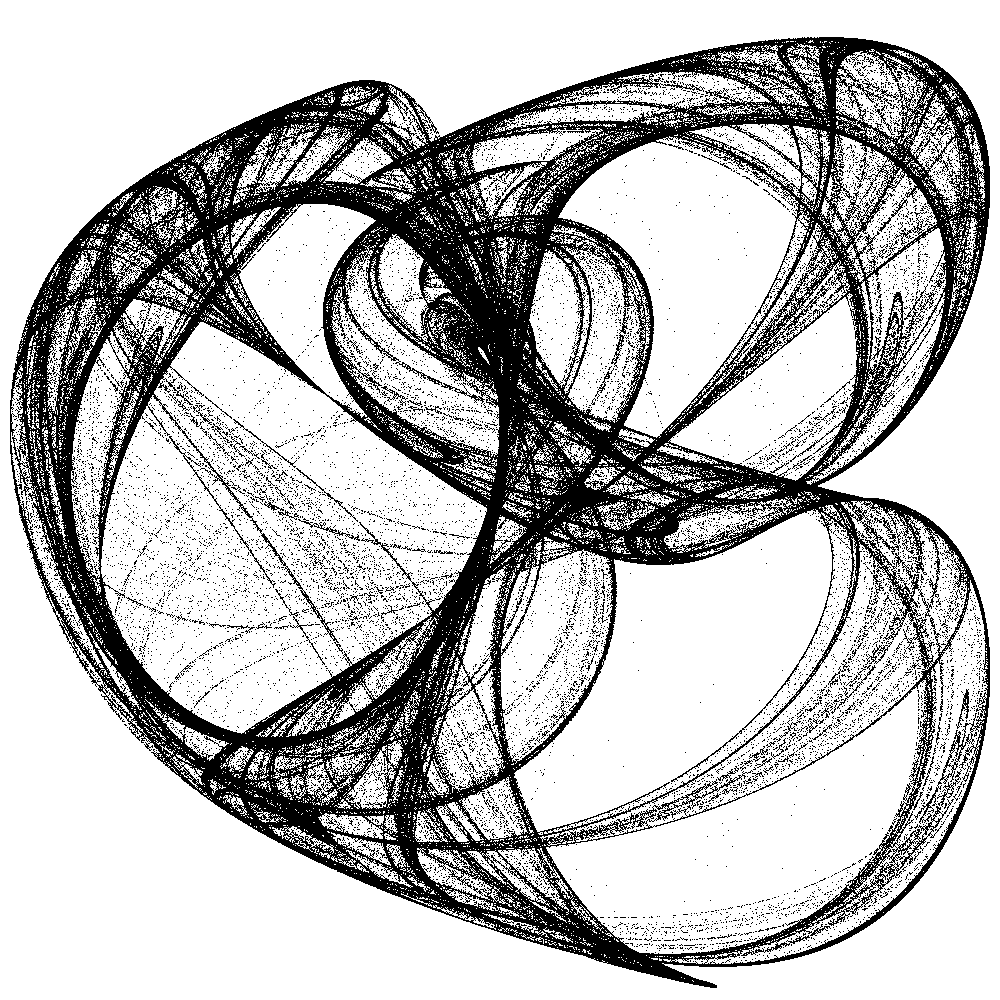 |
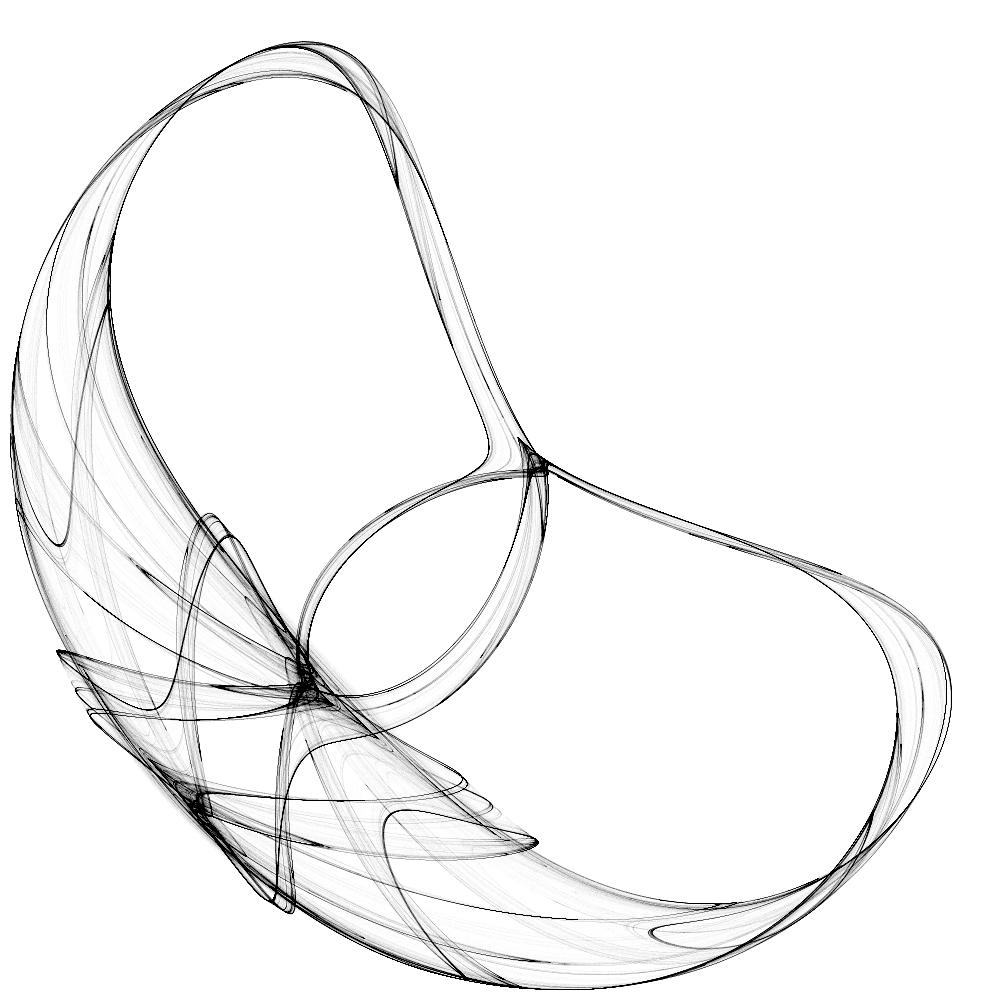
| Abb. 4a: a=1.76, b=1.67, c=-0.86, d=2.10 | Abb. 4b: a=1.76, b=1.67, c=-0.86, d=2.10 |
 |
 |
| Abb. 5a: a=1.268, b=1.441, c=1.235, d=1.492 | Abb. 5b: a=1.268, b=1.441, c=1.235, d=1.492 |
 |
 |
| Abb. 6a: a=2.4, b=1, c=1, d=1 | Abb. 6b: a=2.4, b=1, c=1, d=1 |
 |
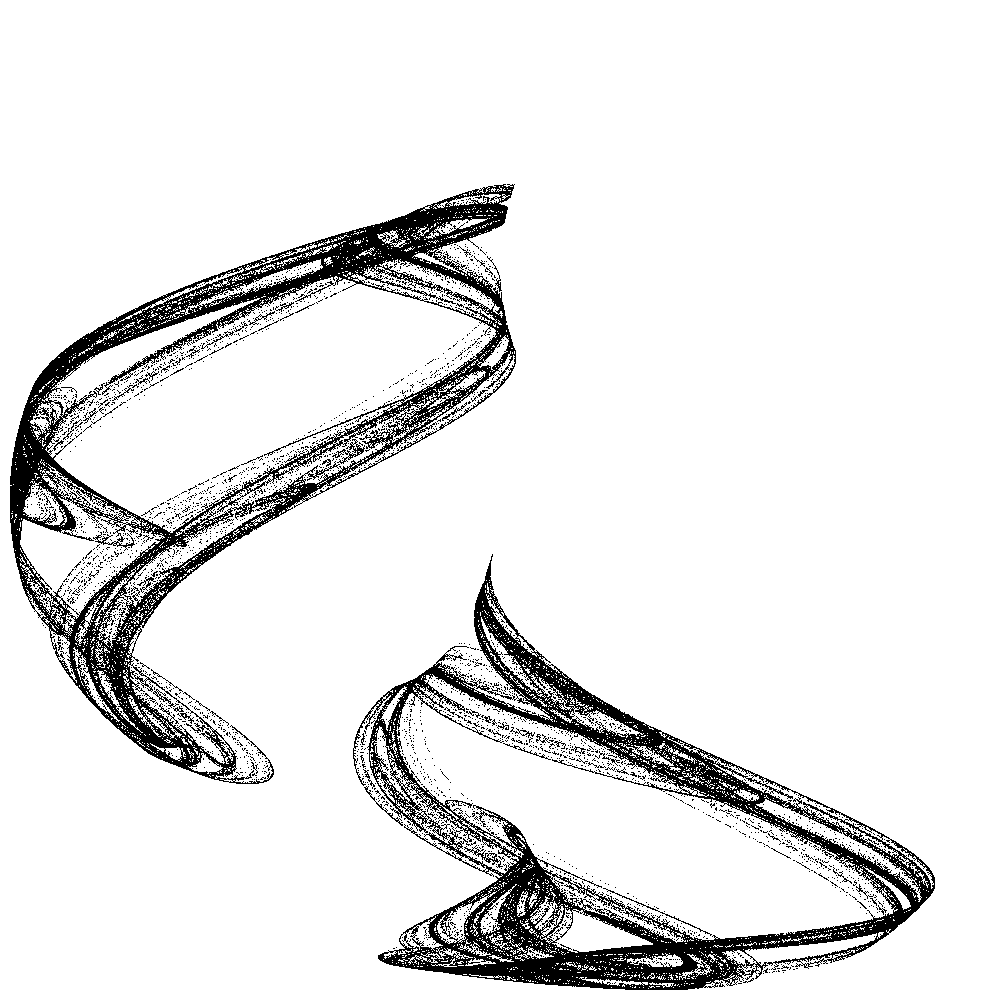 |
| Abb. 7a: a=1, b=2.5, c=1, d=1 | Abb. 7b: a=1, b=2.5, c=1, d=1 |
 |
 |
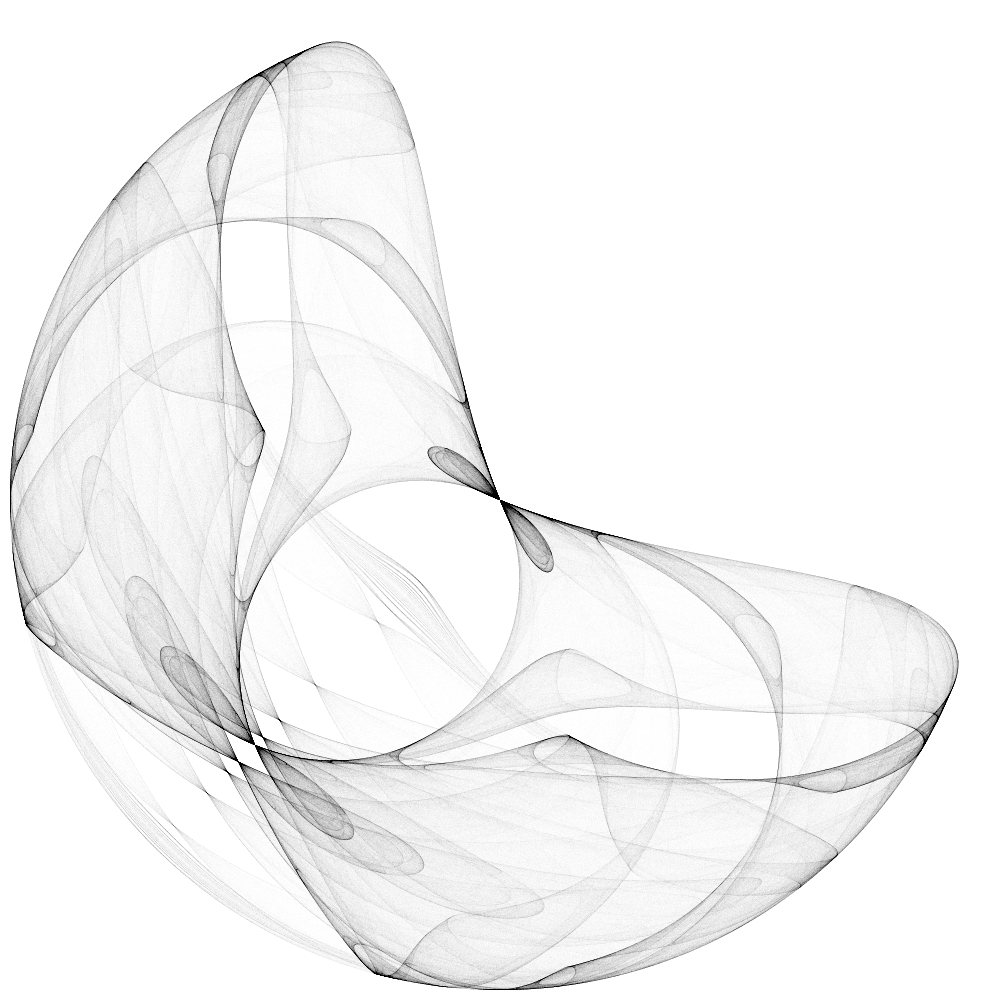
| Abb. 8a: a=1, b=3, c=1, d=1 | Abb. 8b: a=1, b=3, c=1, d=1 |
 |
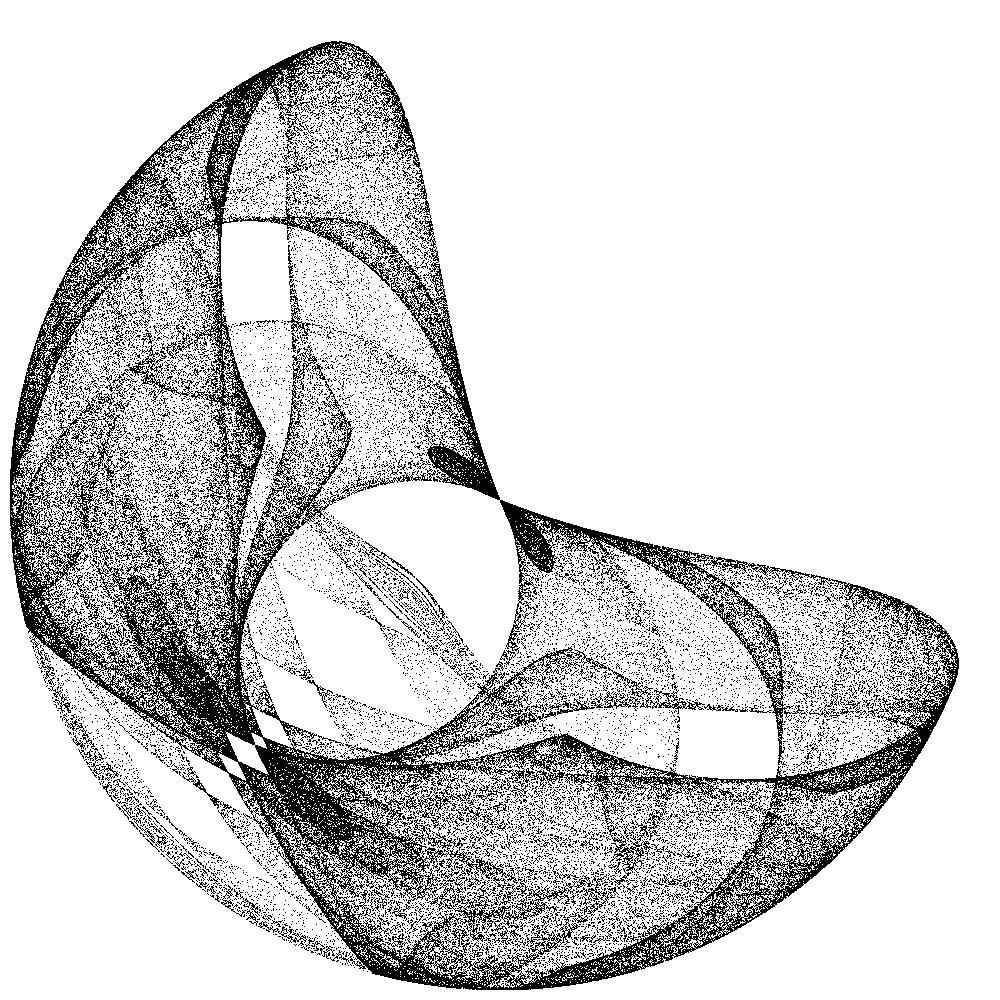 |
| Abb. 9a: a=1.5, b=a, c=a, d=a | Abb. 9b: a=1.5, b=a, c=a, d=a |
 |
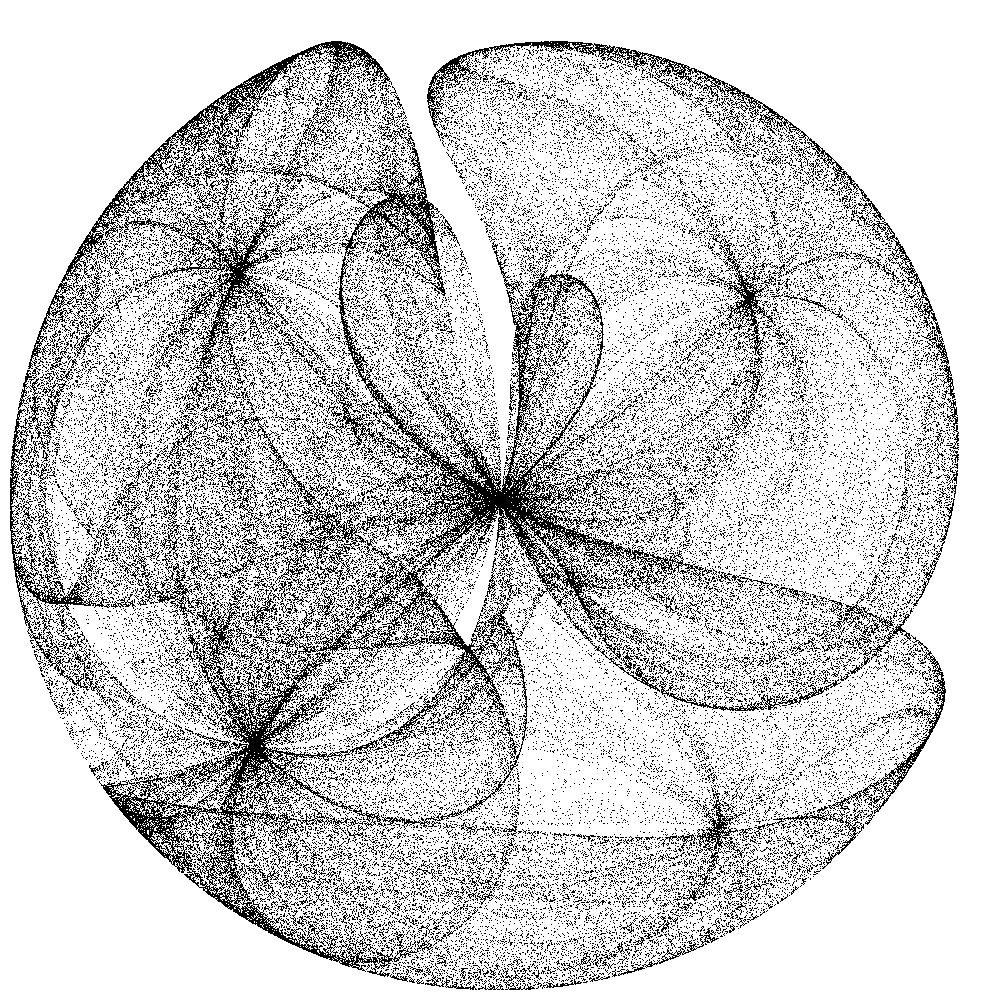 |
| Abb. 10a: a=1.5, b=a, c=-a, d=a | Abb. 10b: a=1.5, b=a, c=-a, d=a |
 |
Abb. 11 (links): a=0..4, b=1, c=1, d=1 Animation der Veränderung des Attraktors, wenn einer der Parameter langsam vergrössert wird. Der variable Paramter hat den angezeigten Wert ±0.05. In diesem Intervall werden zufällig mehrere Werte ausgewählt und die Attraktoren übereinander gezeichnet. Auf diese Weise hat man einen stetigeren Eindruck von der Veränderung. Andernfalls können Sprünge auftreten respl. das Bild kann plötzlich verschwinden. |