Kaustiken am Parabolspiegel

Ein Parabolspiegel sammelt achsenparallel einfallendes Licht im Brennpunkt, aber wie sieht es aus, wenn das Licht schräg einfällt? Was passiert, wenn das einfallende Licht von einer punktförmigen Quelle in kleinem Abstand ausgeht? Die folgenden geometrisch-optischen Simulationen zeigen die entstehenden Kaustiken (Brennlinien). Die Simulationen sind zweidimensional.

Abbildung: Ein Parabolspiegel (Rotationsparaboloid) mit Meridianlinie y = a·x² hat Brennweite f = 1/(4·a). Der Brennpunkt befindet sich auf der Rotationsachse (optische Achse).

Abbildung: Achsenparallel (Einfallswinkel "phi = 0 rad") einfallendes Licht wird im Brennpunkt gesammelt. Es wurden n = 50 Strahlen gezeichnet.

Abbildung: Schiefparallel (Einfallswinkel "phi = 0.1 rad") einfallende Strahlen bilden Hüllkurven (Kaustiken) aus. Es wurden n = 50 Strahlen gezeichnet.

Abbildung: Schiefparallel (Einfallswinkel "phi = 0.3 rad") einfallende Strahlen bilden Hüllkurven (Kaustiken) aus. Es wurden n = 50 Strahlen gezeichnet.

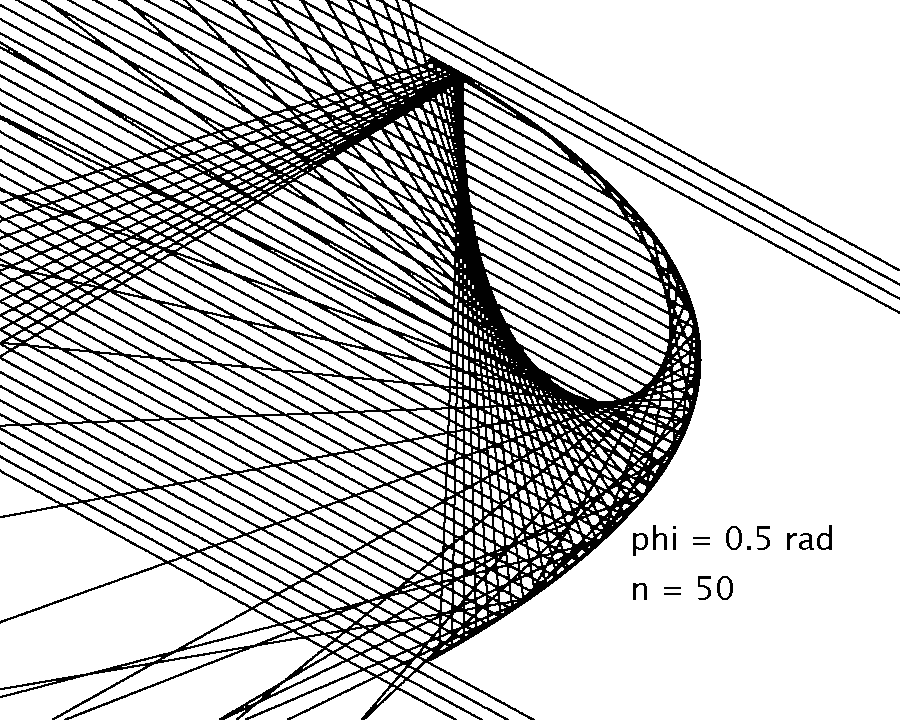Abbildung: Schrägparallel (Einfallswinkel "phi = 0.5 rad") einfallende Strahlen bilden Hüllkurven (Kaustiken) aus. Es wurden n = 50 Strahlen gezeichnet.

In den folgenden Bildern wurde die Dichte der Strahlen als Grauwert codiert.

Abbildung: Achsenparallel (Einfallswinkel "phi = 0 rad") einfallendes Licht wird im Brennpunkt gesammelt. Es wurden n = 10000 Strahlen überlagert.

Abbildung: Achsenparallel (Einfallswinkel "phi = 0 rad") einfallendes Licht wird im Brennpunkt gesammelt. Es wurden n = 10000 Strahlen überlagert. Die Strahlen wurden nicht über den Brennpunkt hinaus fortgesetzt. Man sieht, dass der Brennpunkt nicht von allen Seiten gleichmässig beleuchtet wird.

Abbildung: Schiefparallel (Einfallswinkel "phi = 0.2 rad") einfallendes Licht formt eine Katakaustik. Es wurden n = 10000 Strahlen überlagert.

In den folgenden Bildern ist die Lichtquelle punktförmig. Die Gegenstandsweite g (Abstand Lichtquelle-Parabelscheitel) ist als Vielfaches der Brennweite der Parabel dargestllt. Die Quelle befindet sich auf der optischen Achse des Parabolspiegels.

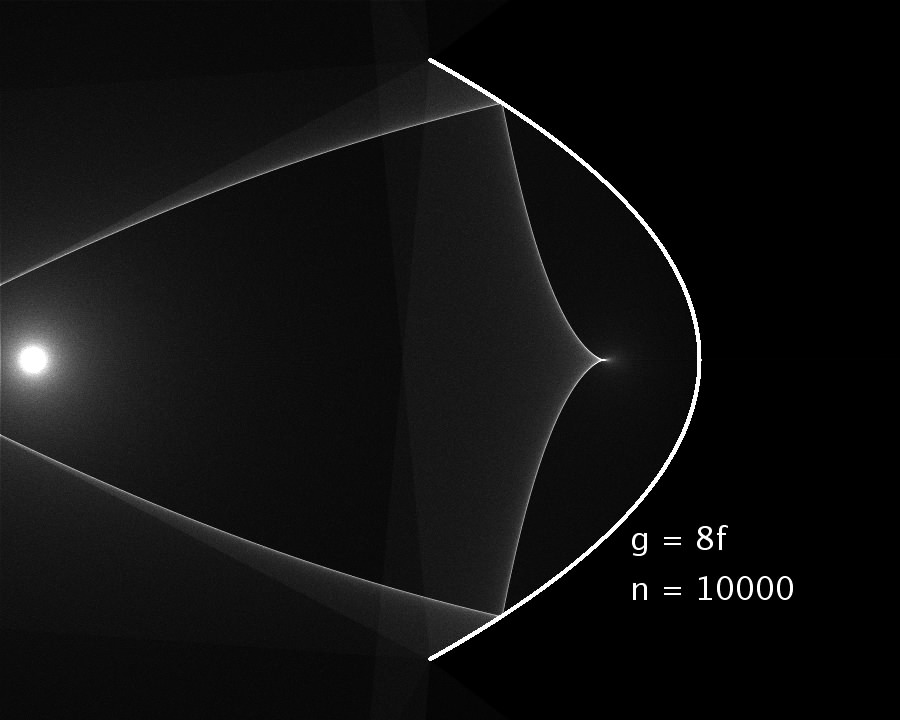Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist 8 mal die Brennweite der Parabel. Es wurden n = 10000 Strahlen überlagert.

Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist 4 mal die Brennweite der Parabel. Es wurden n = 10000 Strahlen überlagert.

Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist 2 mal die Brennweite der Parabel. Es wurden n = 10000 Strahlen überlagert. In der paraxialen Optik fallen in dieser Situation Bild und Gegenstand zusammen.

Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist gleich der Brennweite der Parabel. Es wurden n = 10000 Strahlen überlagert. In dieser Art wird ein Parabolspiegel oft verwendet (Scheinwerferspiegel). Man erkennt, dass die Lichtintensität nicht gleichmässig über den Scheinwerferkegel-Querschnitt verteilt ist, wenn die Lichtquelle in alle Richtungen gleich viel abstrahlt.

Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist die Hälfte der Brennweite der Parabel. Es wurden n = 10000 Strahlen überlagert.

In den folgenden Bildern ist der Quellpunkt nicht mehr auf der optischen Achse des Parabolspiegels. Die Distanz zur optischen Achse ist als Vielfaches der Brennweite ausgedrückt (eine Brennweite Abstand).

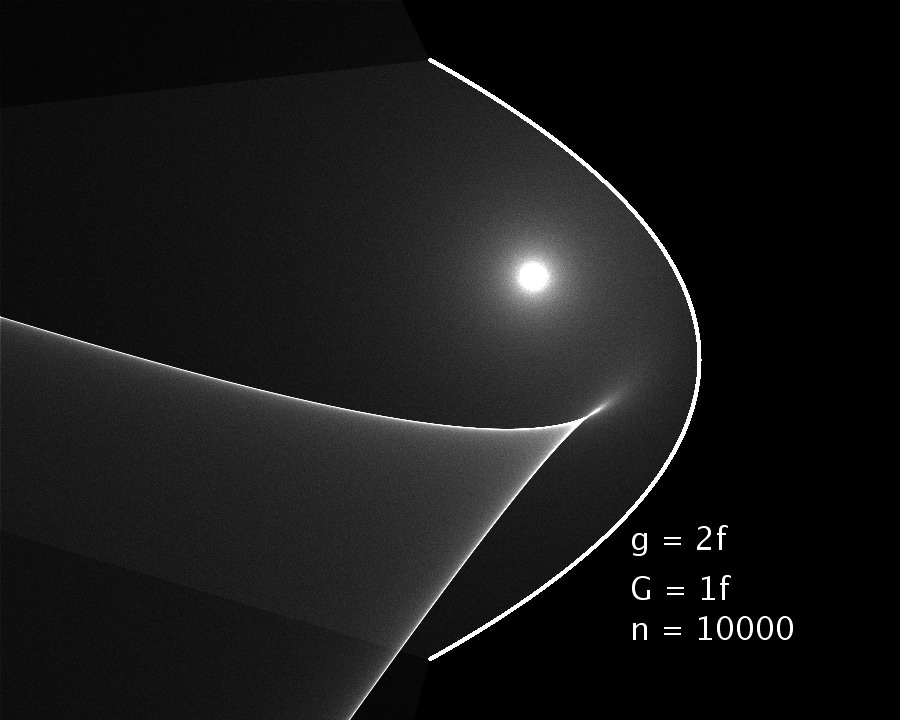
Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist 2 mal die Brennweite der Parabel. Die Quelle ist G = 1 Brennweite von der optischen Achse entfernt. Es wurden n = 50 Strahlen überlagert.

Abbildung: Licht von einer punktförmigen Quelle wird an einer Parabel reflektiert. Der Abstand Parabelscheitel-Lichtquelle (Gegenstandsweite g) ist 2 mal die Brennweite der Parabel. Die Quelle ist eine Brennweite von der optischen Achse entfernt. Es wurden n = 10000 Strahlen überlagert.

Abbildung: Diffuses Licht trifft auf den Parabolspiegel. Das einfallende Licht hat statistisch gleichmässig verteilte Richtungen (nach rechts) und Startpositionen (links von der Parabelöffnung). Es sind keine prominenten Intensitätserhöhungen erkennbar. Wer genau hinschaut, kann noch ein paar schwache Programmierfehler erkennen.

erste Version: 4. Oktober 2008, letzte Änderung: 5. Oktober 2008 / Martin Lieberherr

Zum Seitenanfang