 |
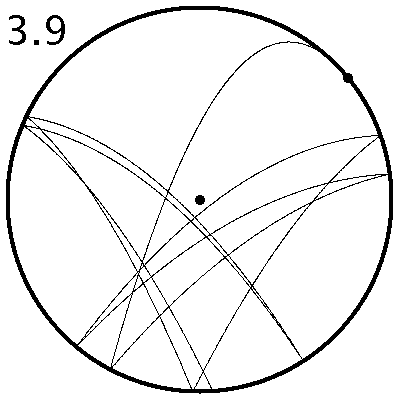
| Abbildung 1: Bahn des Fadenpendels für den Kontrollparameter f=3.9 (links oben im Bild). Kreiszentrum und Ablösestelle sind mit einem fetten Punkt markiert. Die Bahn ist chaotisch, d.h. würde man mehr Parabeln zeichnen lassen, so wäre allmählich der ganze Kreis bis zur maximal erreichbaren Höhe fr/2 schwarz eingefärbt. |
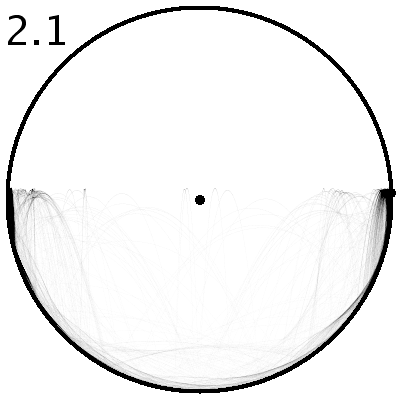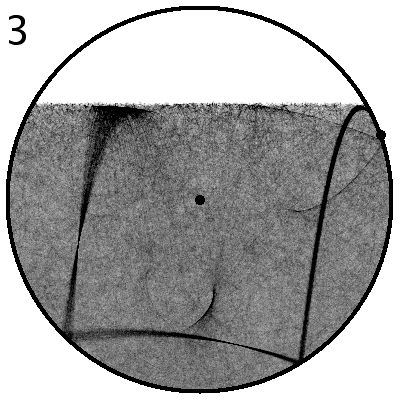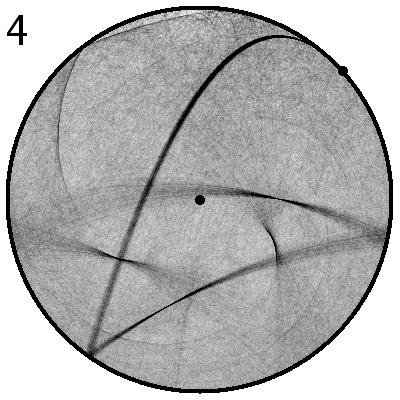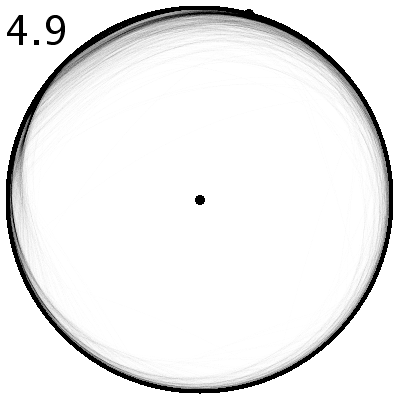 |
| Abbildung 2: Animation des chaotischen Verhaltens (animated gif mit 2.9 MByte) Der Kontrollparameter wird von f=2.1 bis f=4.9 in Schritten von 0.1 gesteigert. Bei jedem Wert werden 400 Bahnen à 50 Parabelbögen berechnet, wobei der Startwert leicht variiert wird (±0.01 des Kontrollparameters). Die Dichte der Bahnen (Aufenthaltswahrscheinlichkeit) ist als Grauwert codiert. An gewissen Stellen deuten sich Hüllkurven oder Häufungspunkte an. Der allgemeine Eindruck ist jedoch, dass der energetisch zugängliche Bereich gleichmässig grau eingefärbt ist, d.h. die Bewegung ist hoch chaotisch. (Denselben Eindruck ohne Hüllkurven erhält man, wenn Tausende von Parabelbögen für einen einzigen Parameterwert f gezeichnet werden.) |
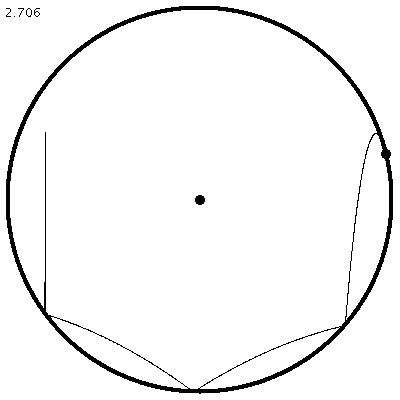 |
| Abbildung 3: Periodische Bahn, die in sich selbst zurückläuft (die spiegelsymmetrische, zweite Hälfte ist nicht gezeichnet). |
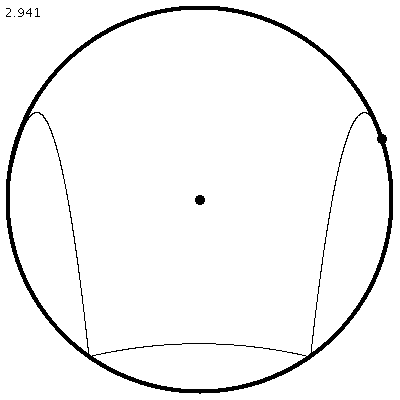 |
| Abbildung 4: Periodische Bahn, die immer im gleichen Sinn durchlaufen wird. |
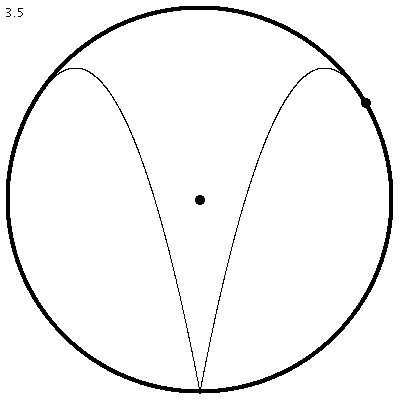 |
| Abbildung 5: Periodische, symmetrische Bahn mit einer einzigen Reflexion, die immer im gleichen Sinn durchlaufen wird. |
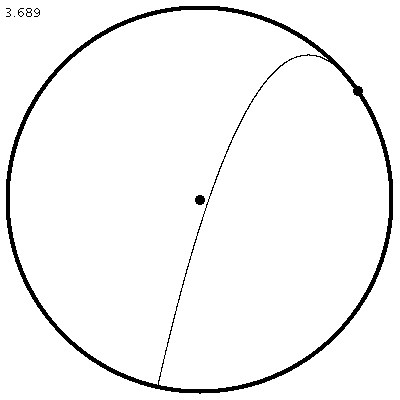 |
| Abbildung 6: Periodische, symmetrische Bahn, die in wechselnder Richtung durchlaufen wird (nur eine Hälfte ist gezeichnet). |
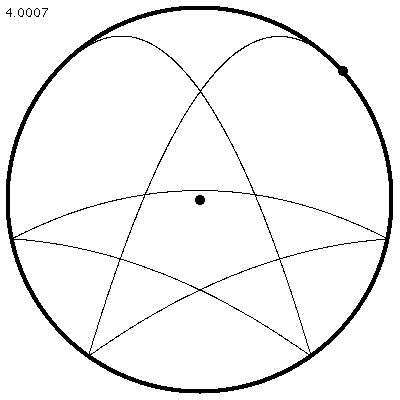 |
| Abbildung 7: Periodische Bahn mit vielen Reflexionen. Zwischendurch bewegt sich das Pendel immer wieder mal dem Kreis entlang, d.h. der Faden ist gestreckt. |
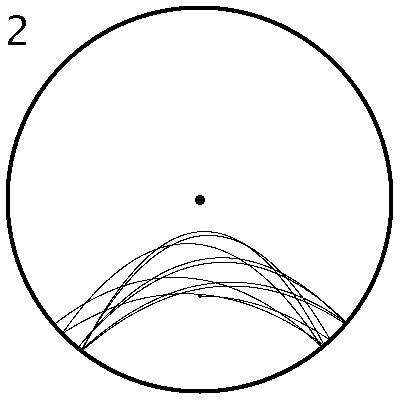 |
| Abbildung 8: Chaotische Bahn des mathematischen Fadenpendels |
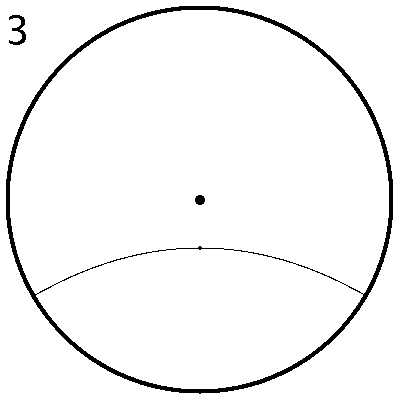 |
| Abbildung 9: Periodische Bahn des mathematischen Fadenpendels |