Kepler-Isochronen

Seit Kepler weiss man, dass sich Planeten auf Ellipsenbahnen um die Sonne bewegen. Die Form der Ellipse ist einfach zu beschreiben, aber die Position eines Planeten zu einem bestimmten Zeitpunkt muss mit der nichtlinearen Kepler-Gleichung berechnet werden. Es ist heute einfacher, die Kräfte mit dem Newtonschen Gravitationsgesetz zu bestimmen und anschliessend F=ma (Bewegungsgleichung) numerisch zu integrieren, z.B. wie unten mit dem Euler-Cromer Verfahren.

Sei T die Umlaufzeit des Planeten, a die grosse Halbachse seiner Bahn, G die Newtonsche Gravitationskonstante, M die Masse des Zentralkörpers, m die Masse des Planeten, v seine Bahngeschwindigkeit und r der Abstand Sonne-Planet. Die Masse des Planeten sei wesentlich kleiner als die Masse der Sonne. Dann gilt
E_total = -GMm / (2a) = -GMm/r + ½·mv² (Die Gesamtenergie ist erhalten und bei gebundenen Bahnen negativ.)
a³ / T² = GM / (2π)² (drittes Keplersches Gesetz)
Aus diesen Gleichungen folgt, dass Bahnen gleicher Energie auch gleiche Umlaufzeiten haben.

Nun folgen einige numerisch erstellte Graphiken zum Thema:

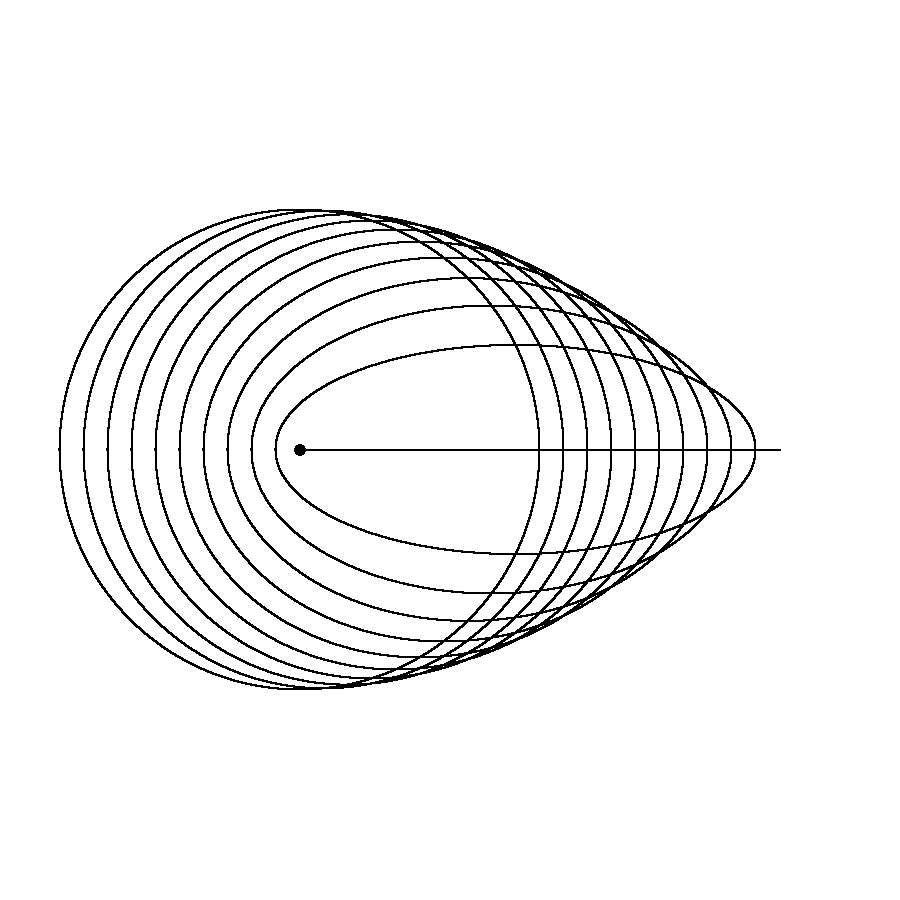
1. Abbildung: Keplerbahnen gleicher Umlaufzeit T respektive gleicher grosser Halbachse a. Der Aphel aller Bahnen liegt auf der Halbgeraden rechts von der Sonne. Die Sonne ist als fetter Punkt eingezeichnet. Die Exzentrizitäten laufen von ε = 0 (Kreis mit Radius a) bis ε = 1 (Strecke der Länge 2a).

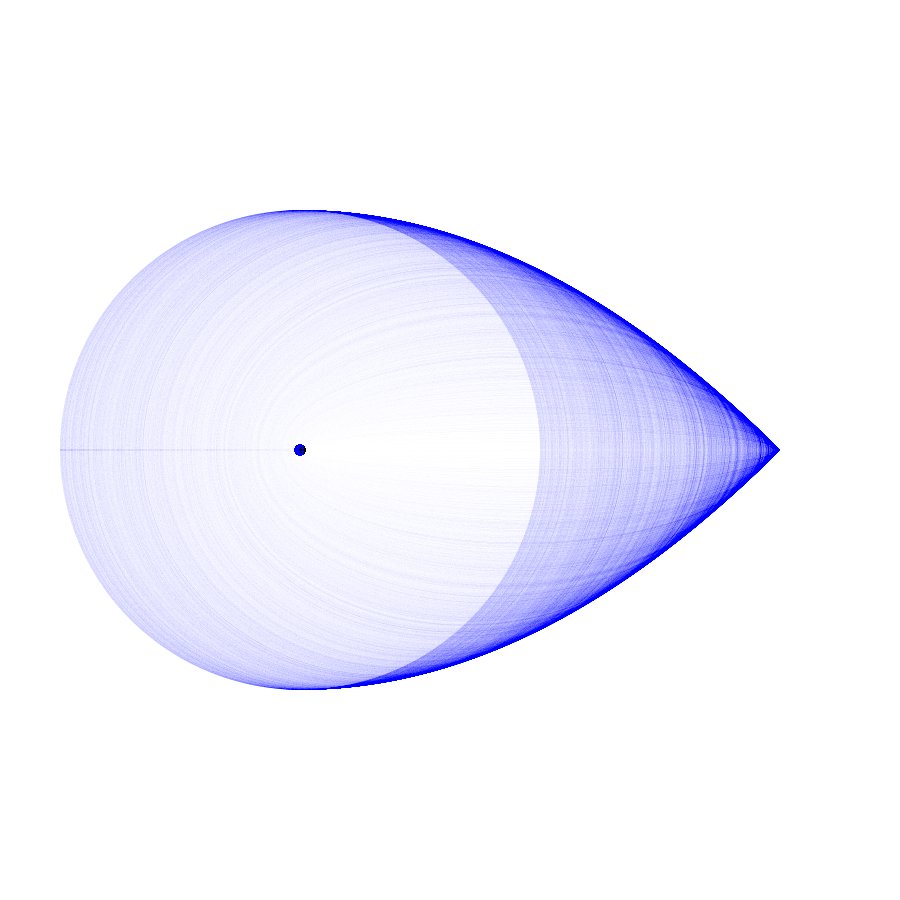2. Abbildung: Gleiche Situation wie vorher in Abbildung 1, aber mit viel mehr gezeichneten Bahnen und der Dichte der Bahnen als Helligkeit kodiert: Je dunkler die Stelle desto dichter sind die Bahnen respektive desto länger halten sich die Massenpunkte dort auf.

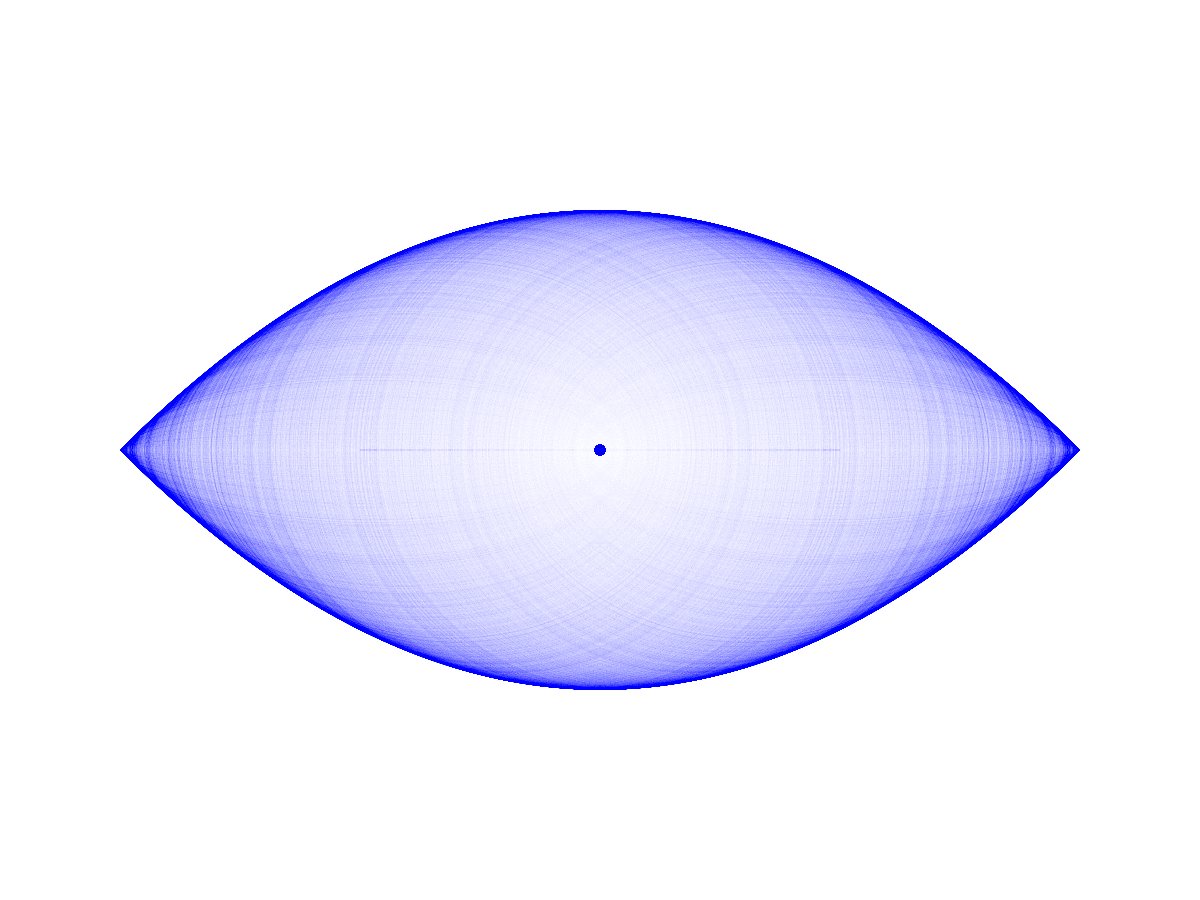3. Abbildung: Gleiche Situation wie vorher in Abbildung 2, aber die Bahnen mit Aphel auf der linken Seite sind ergänzt. Die Einhüllende aller Ellipsen besteht aus zwei Parabeln.

Die Ellipsenbahnen werden mit variabler Geschwindigkeit durchlaufen. Verbindet man die Positionen auf einer Ellipsenschar, welche die Testkörper zu gleichen Zeitpunkten einnehmen, so erhält man Isochronen (Kurven gleicher Zeit). Wie sehen diese Isochronen aus?

4. Animation: 100 Massenpunkte starten im Aphel rechts von der Sonne nach oben wie in Abbildung 1 und 2. Alle Bahnen haben gleiche Energie respektive Umlaufzeit. Der Abstand zweier Frames des animated gif ist ein Hundertstel der Umlaufzeit. Jener Massenpunkt, der am nächsten im Abstand a von der Sonne startet, bewegt sich auf einer Kreisbahn. Jener Massenpunkt, der am weitesten rechts im Abstand 2a von der Sonne startet, fällt direkt auf die Sonne zu.

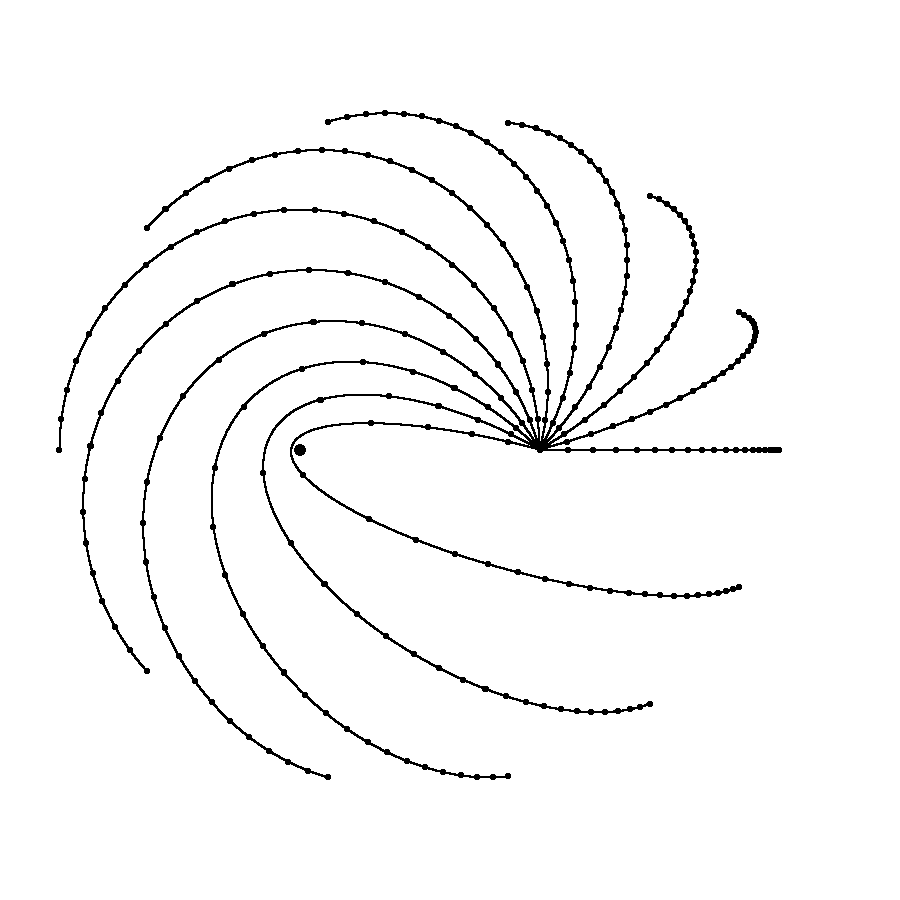5. Abbildung: Zwölf Massenpunkte starten am gleichen Ort in zwölf verschiedene Richtungen und laufen um die Sonne. Die Sonne ist als fetter Punkt dargestellt. Die elliptischen Bahnen sind für eine halbe Umlaufzeit gezeichnet. Die Anfangsgeschwindigkeit ist im Betrag für alle gleich, nämlich gleich der Bahngeschwindigkeit (Schnelligkeit) auf einer Kreisbahn. Eine der Bahnen ist deshalb kreisförmig. Nach jeweils 1/25 der Umlaufzeit ist die Position mit einem fetten Punkt markiert. Die Markierungen sind nicht gleichabständig, denn eine Planetenbahn wird in Sonnennähe schneller durchlaufen als in Sonnenferne.

6. Animation: 100 Massenpunkte starten rechts der Sonne in 100 verschiedene Richtungen in die obere Hälfte der Darstellung, wie in Abbildung 5. Die Bahngeschwindigkeit am Start ist bei allen gleich. Eine der Bahnen ist kreisförmig. Der zeitliche Abstand zwischen zwei Frames des animated gif ist ein Hunderstel der Umlaufzeit. Jeder Massenpunkt verfolgt seine eigene Ellipsenbahn.

erste Version: 16. Oktober 2013, letzte Änderung: 17. Oktober 2013 / Martin Lieberherr

Zum Seitenanfang oder Zurück zur Startseite