Epizykeltheorie

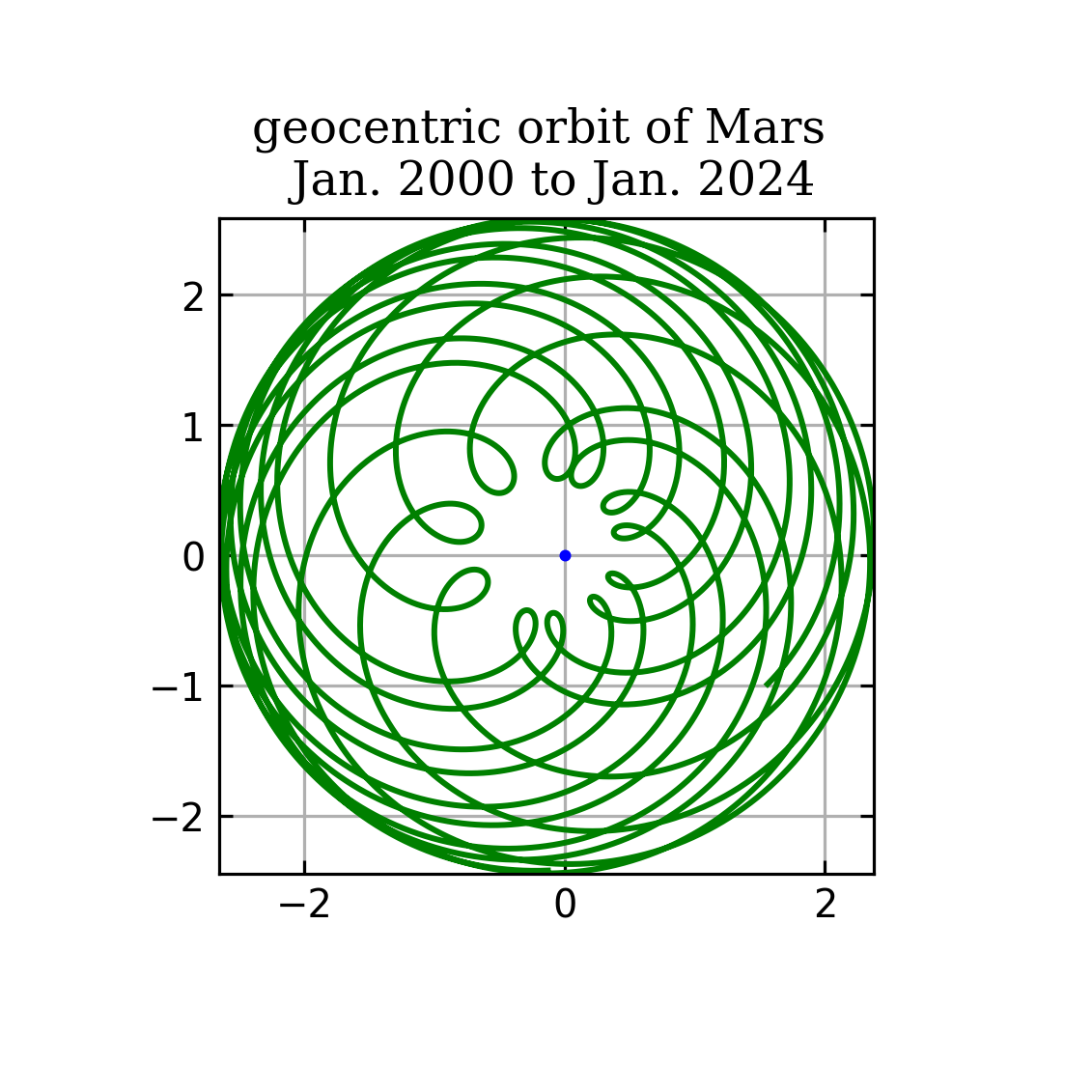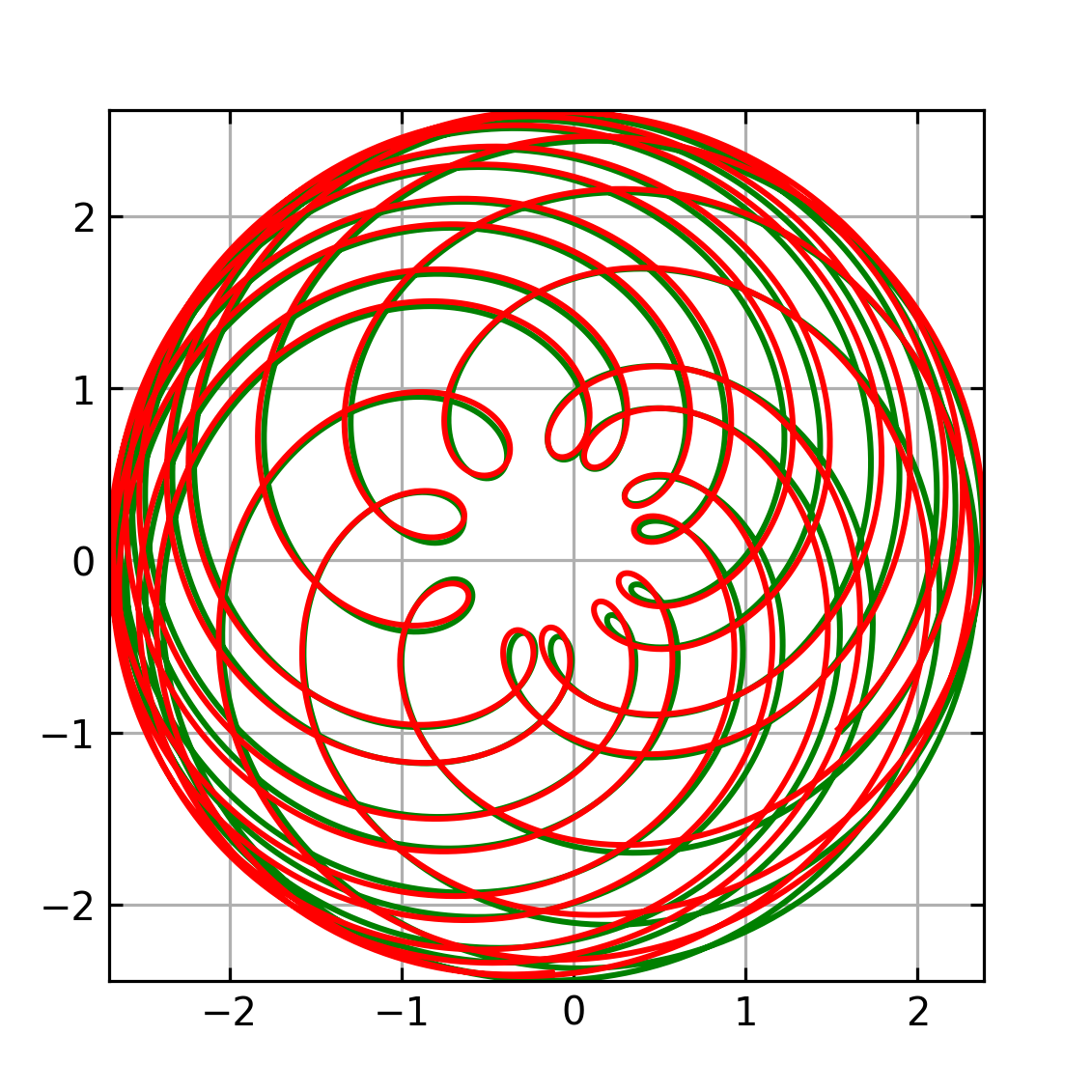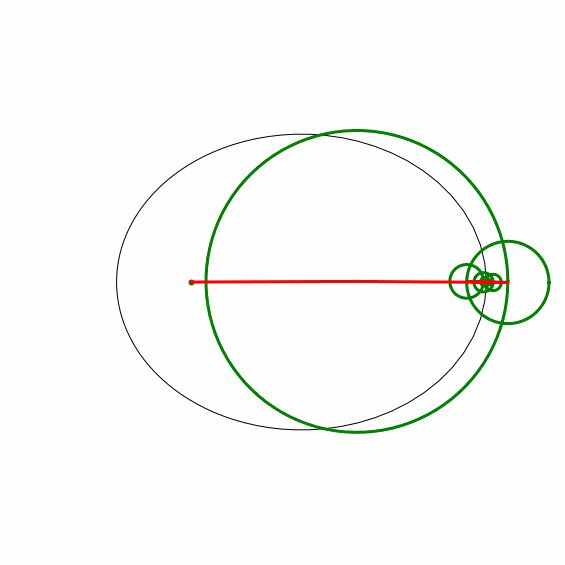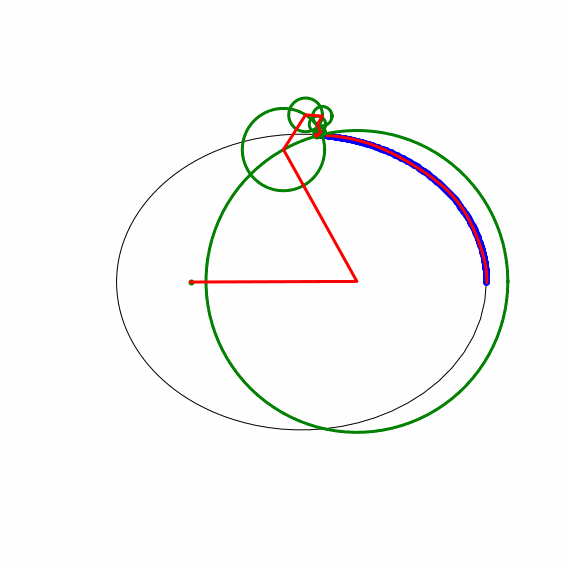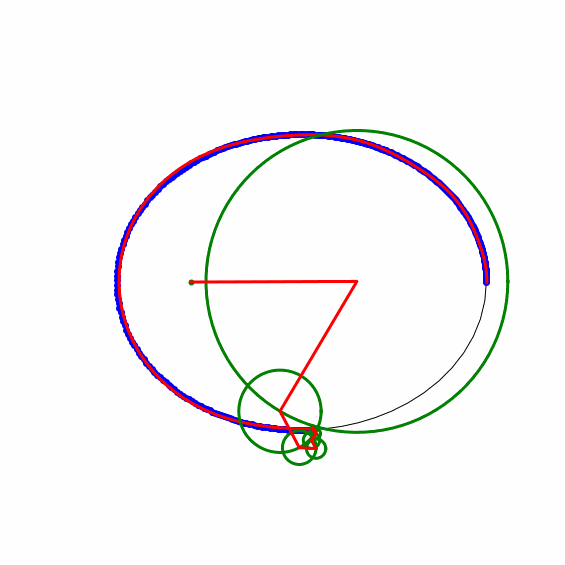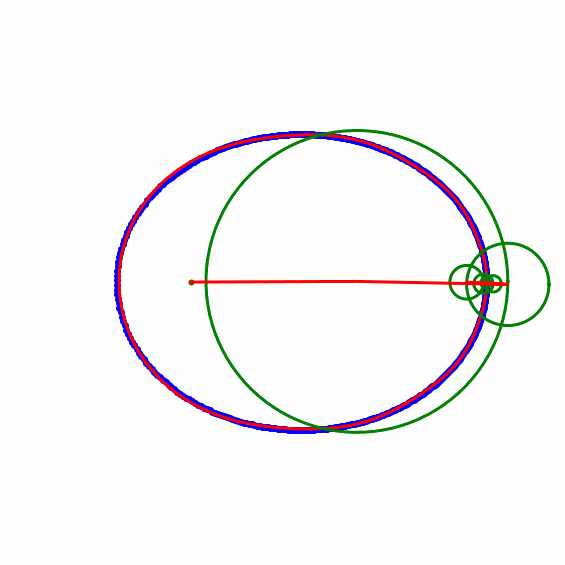
Animation 1: Heliozentrische, keplersche Ellipsenbahn approximiert durch eine komplexe Fourierreihe. Die Koeffizienten der Fourierreihe tragen die Nummern -7, -6, .. , 5, 6, 7. Dies bedeutet, dass 14 Kreisbewegungen kombiniert sind, wobei einige Kreise sehr kleine Radien haben. Die Keplerbahn wurde in Python numerisch integriert, dann Fourier-analysiert, dann die Fourierreihe für viele Zeitpunkte ausgewertet und als animated gif gespeichert. Der erste Kreis (Deferent) hat als Zentrum den Schwerpunkt der Bahnpunkte, die laufenden Kreise (Epizykel) werden nach absteigendem Radius addiert. Die Ellipse ist als dünne, schwarze Linie gezeichnet, die zeitlich gleichabständigen Positionen auf der Bahn als blaue Kreise, die via Fourierreihe berechnete Bahn ist als rote Linie darüber gelegt. Die Kreise sind in grün und deren Radien in rot dargestellt.

Animation 2: Das Video eines Schriftzugs wurde grob getrackt und dann die Bewegung durch Kreisbewegungen approximiert. Jede periodische Bewegung in der Ebene kann als Kombination von Kreisbewegungen dargestellt werden. Damit Standard-Fourieranalyse angewendet werden kann, sollten die Bahnpunkte zeitlich gleichabständig sein.

Abbildung 3: Geozentrische Bahn des Planeten Mars vom 1. Januar 2000 bis 1. Januar 2024 in 1-Tages-Abständen. Die Koordinaten sind in astronomischen Einheiten. Sie wurden berechnet mit https://ssd.jpl.nasa.gov/horizons/ und dann in Python importiert sowie graphisch dargestellt.

Abbildung 4: Geozentrische Bahn von Mars während 23 Jahren (grüne Linie, wie in Abbildung 3) mit einer Approximation durch gleichmässige Kreisbewegungen (rote Linie) Da die geozentrische Bewegung nicht periodisch ist, wurden zwei Fourierreihen kombiniert. Die komplexe Fourierreihe für die Erde hat die Koeffizienten mit Nummern -2, -1, 0, +1, +2, i.e. vier Kreisbewegungen, davon je zwei gegenläufige mit gleicher Frequenz. Die Reihe für Mars hat die Koeffizienten mit Nummern -3, -2, ..., +2, +3, d.h. sechs Kreisbewegungen wovon je zwei gegenläufige gleicher Frequenz.

Animation 5: Geozentrische Bewegung von Mars mit Approximation nach Abbildung 4. Die wahre Bewegung ist als grüne Line, die durch Kreisbewegungen approximierte Bewegung als rote Line dargestellt. Die Marken am Bahnende zeigen momentane Positionen an. Wird die Zahl der Kreisbewegungen erhöht, so wird die Approximation besser.