Kaustiken im elliptischem Spiegel
Ein leuchtender Punkt (Lichtquelle) befindet sich im Innern eines elliptischen Spiegels. Liegt er auf einem der Brennpunkte, so wird das Licht zum anderen Brennpunkt hin reflektiert. Der eine Brennpunkt wird also auf den anderen abgebildet. Aber was passiert, wenn der Quellpunkt anderswo liegt? Wie die Bilder unten zeigen, bildet sich in den meisten Fällen eine mehr oder weniger komplizierte Kaustik (Brennlinie).
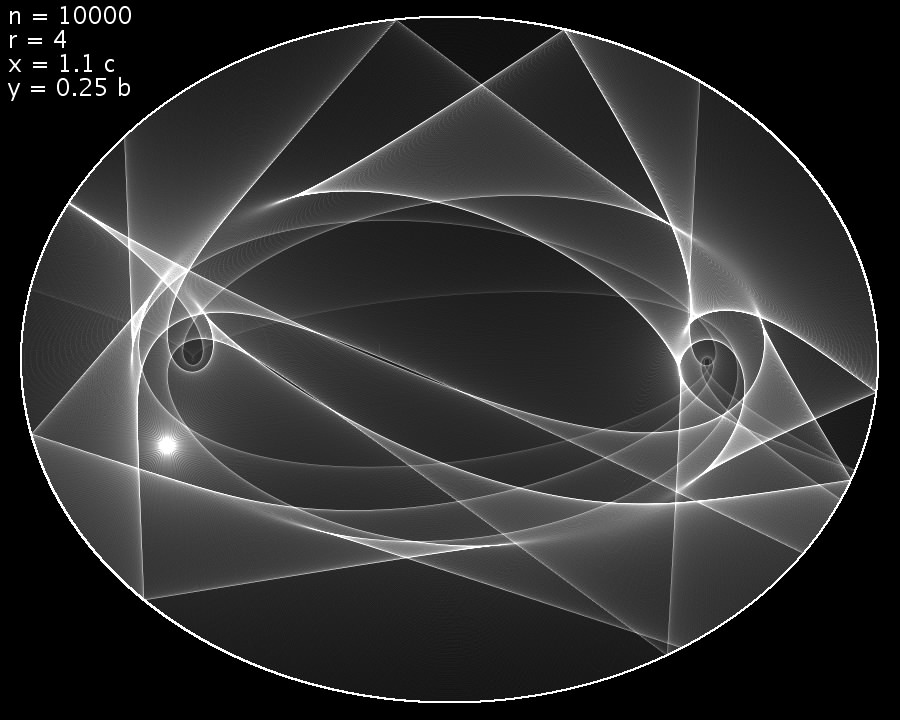
Das erste Bild zeigt, was gerechnet wurde. Die Parameter sind oben links im Bild eingezeichnet. Es sind n = 1 Strahlen, die r = 2 Reflexionen erfahren. Sie starten im Quellpunkt mit Koordinaten x = 1.1 c (links) und y = 0.25 b (unten) relativ zum Ellipsenmittelpunkt. Dabei ist b die kleine Halbachse und c die lineare Exzentrizität (c2 = a2 - b2 mit grosser Halbachse a). Der Brennpunkt befindet sich bei x = c und y = 0.
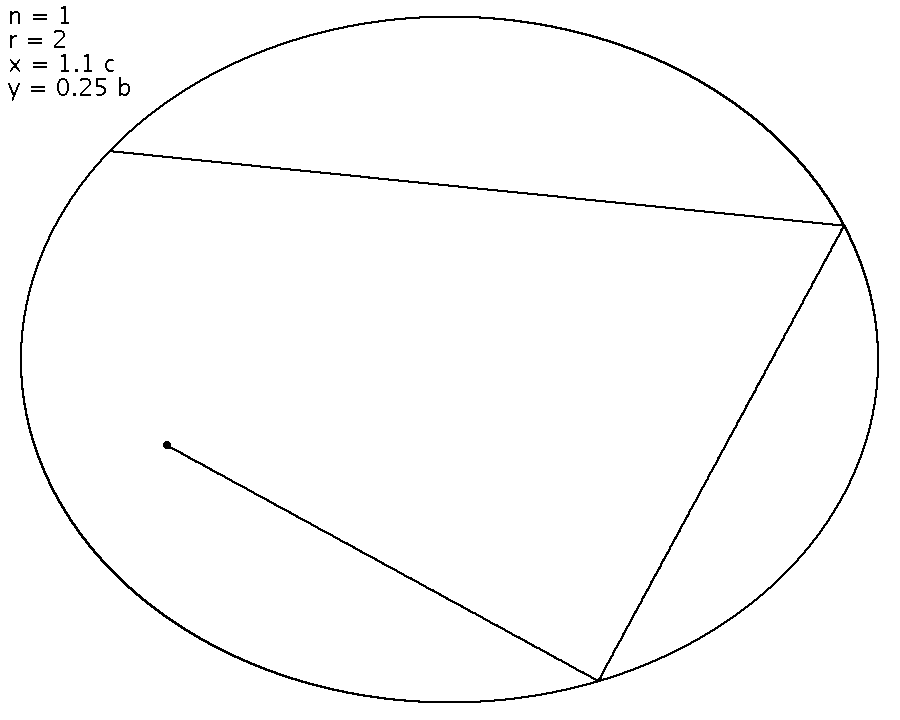
Werden mehrere Strahlen in dasselbe Bild gezeichnet, so erscheinen Hüllkurven der reflektierten Strahlen. Die Strahlen werden nicht mehr in einem Punkt gebündelt, sondern bilden eine Kaustik (Brennlinie, entspricht der Hüllkurve). Ein Punkt wird also durch einen elliptischen Spiegel nicht mehr auf einen Punkt abgebildet.
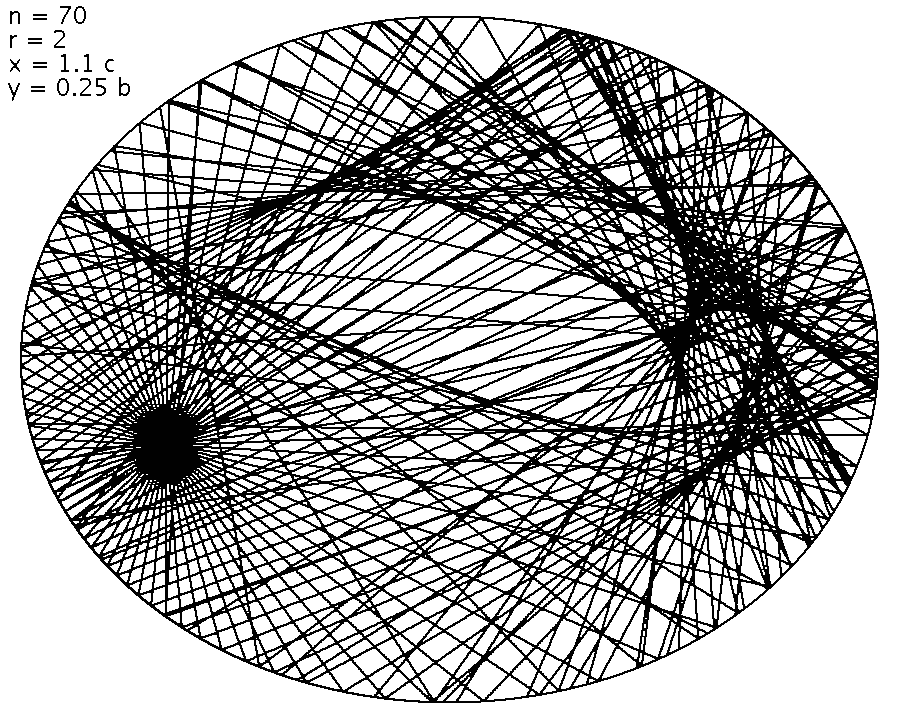
Damit die Bilder schöner werden, habe ich viel mehr Strahlen eingezeichnet und die Dichte der Strahlen als Grauwert codiert. Grosse Helligkeit bedeutet dann viel Licht. Dafür habe ich meist nur noch eine einzige Reflexion gerechnet.
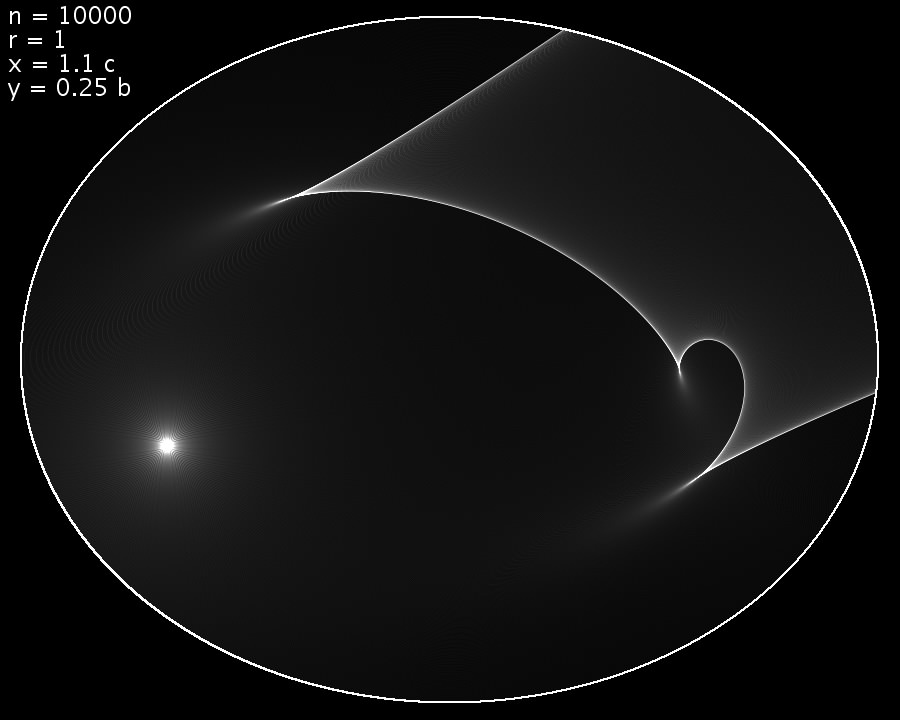
Gelegentlich berücksichtigte ich bis zu vier Reflexionen.
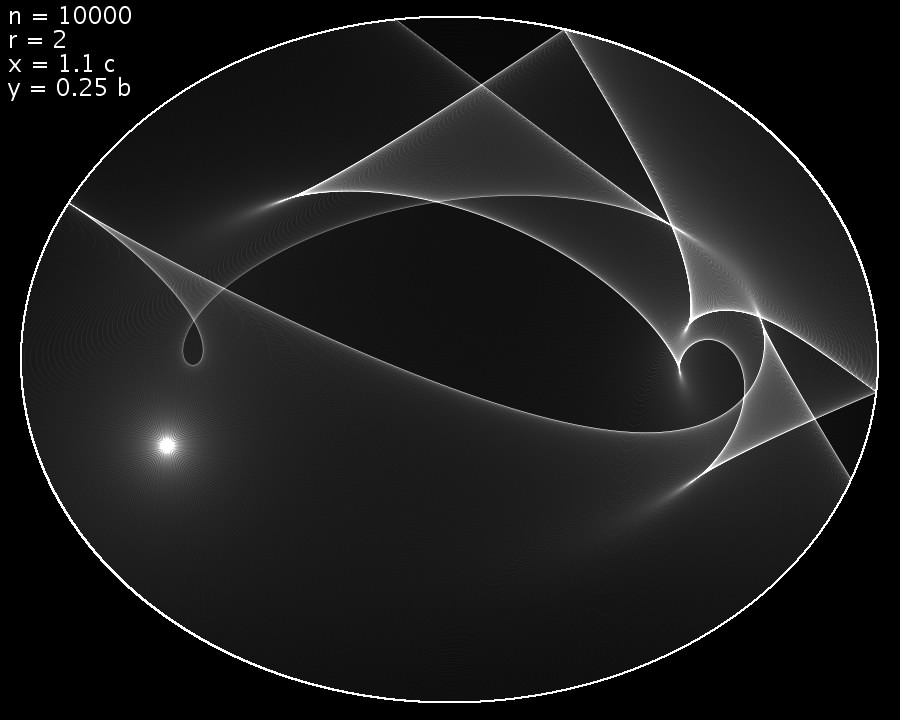

Wer sich für die Berechungen interessiert, kann hier das Programm herunterladen: Ellipsenkaustik.txt
Es handelt sich um ein Programm in METAL-Basic für einen iMac G4 unter Betriebssystem OS 10.2.8. Das Programm wurde als Textfile abgespeichert, damit man den zentralen Teil lesen kann. Der Grafikteil ist sicher maschinenabhängig, aber die Rechnungen dürften sich mit mässigem Aufwand auf andere Maschinen und Programmiersprachen übertragen lassen. Das Programm erzeugt (riesige) PICT-Files, die ich nachher mit einem Grafikprogramm in (kleine) JPG-Files umwandelte. Die Berechung eines Bildes dauert mehrere Minuten.
Wenn Sie dem Link folgen, sehen Sie eine Animation, in der sich der Quellpunkt von der Ellipsenmitte entlang der grossen Halbachse bewegt
(1 sec pro frame, 2.5 Megabyte, animated gif):
Kaustik_anim_a.gif
Und in folgender Animation bewegt sich der Quellpunkt vom Brennpunkt aus parallel zur kleinen Halbachse
(1 sec pro frame, 1.3 Megabyte, animated gif): Kaustik_anim_b.gif
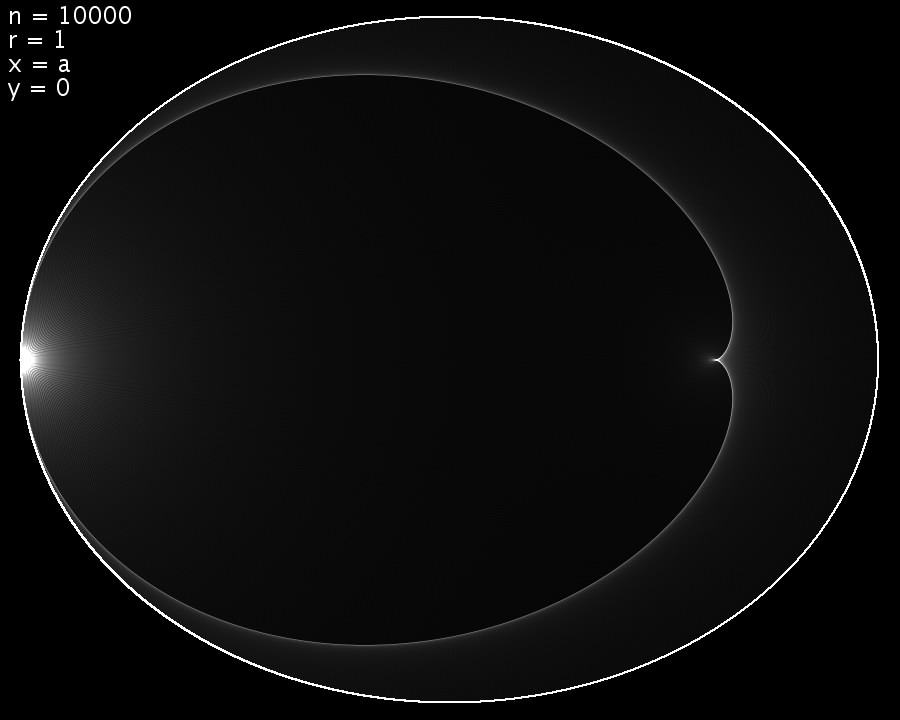
Im folgenden Bild befindet sich der Quellpunkt am Hauptscheitel. Die Kaustik hat dann nur eine Spitze. Dort befindet sich in paraxialer Näherung das Bild des Quellpunkts. Der Krümmungsradius im Hauptscheitel ist r = b2/a, die Brennweite des Spiegels ist f = r/2. Mit Hilfe der Abbildungsgleichung könnte man die Lage des Bildes ausrechnen.
Das folgende Bild zeigt einen Spezialfall des Spezialfalls: Die Ellipse ist ein Kreis und der Quellpunkt befindet sich am Kreisrand. Die Spitze der Kaustik ist in paraxialer Näherung das Bild des Quellpunkts. Die Brennweite des Spiegels ist f = r/2. Aus der Gegenstandsweite 2r erhält man die Bildweite 2r/3.

Die Kaustik im vorangehenden Bild scheint eine bekannte Form zu haben: jene einer Kardioiden (Herzkurve). Legt man wie in der folgenden Abbildung eine Karioide (Punkte) über die Kaustik, so scheint sie gut zu passen. (Man kann das auch beweisen.)

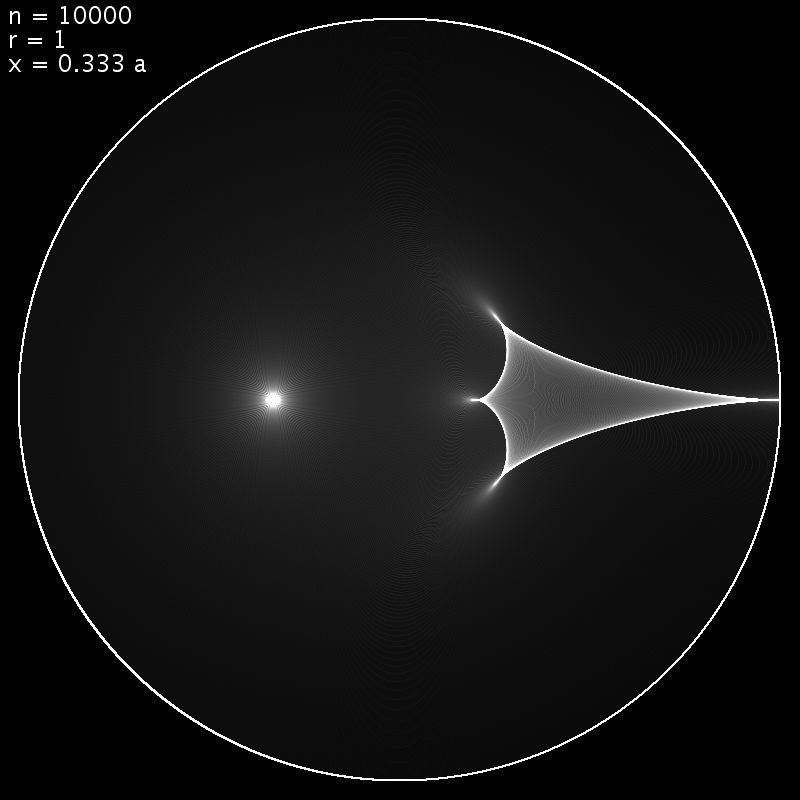
Im folgenden Bild wird die Kaustik von einem Quellpunkt gebildet, der r/3 vom Kreiszentrum entfernt ist. Die innere Spitze der Kaustik ist r/5 vom Zentrum entfernt, die äussere, rechte Spitze entsteht durch Abbildung der Quelle via die linke Kreishälfte und liegt genau auf dem Rand. Die obere Spitze entstehen bei Abbildung der Quelle durch die obere Kreishälfte, analog die untere Spitze durch Abbildung an der unteren Kreishälfte.
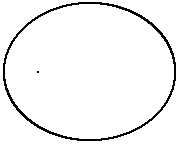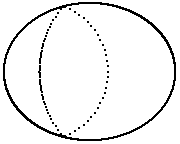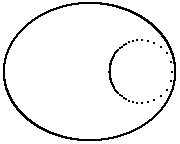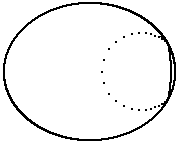
Zum Schluss noch der Normalfall: Brennpunkt wird auf Brennpunkt abgebildet.

Offensichtlich wird der 2. Brennpunkt (rechts) nicht gleichmässig beleuchtet, obwohl die Quelle (links) in alle Richtungen gleich abstrahlt. Die folgende Animation verdeutlicht dies: 80 Lichtstrahlen starten beim ersten Brennpunkt in alle Richtungen gleichmässig. Gezeichnet wird die sich ausbreitende Wellenfront, d.h. die Spitzen der Lichtstrahlen zu jeweils gleichen Zeiten. Man sieht, dass die Strahlen nicht aus allen Richtungen gleichmässig in den anderen Brennpunkt einlaufen.
Erste Version: 20. Mai 2007 / Martin Lieberherr
Ergänzungen: 23. August 2007, 8. Nov. 2008, 31. Mai 2010 / Lie.











