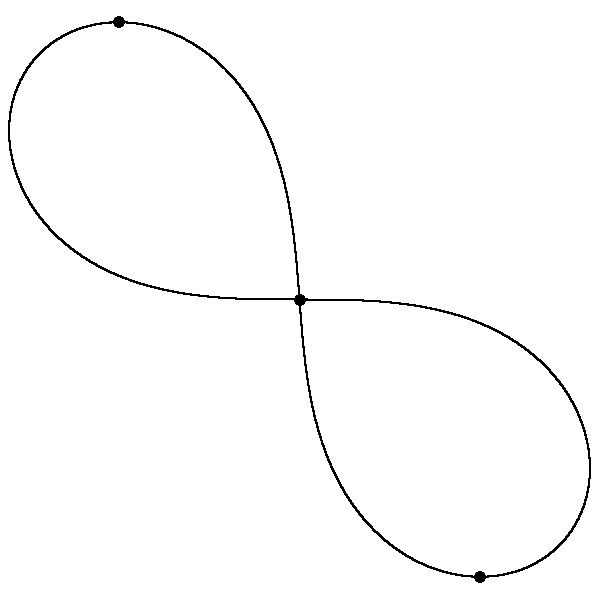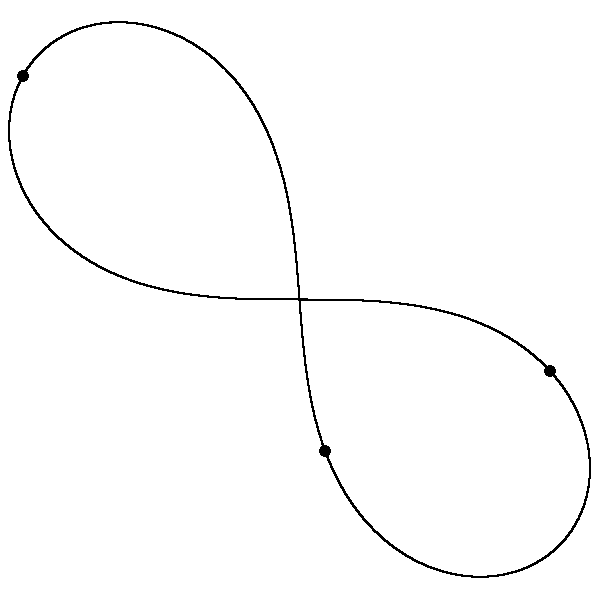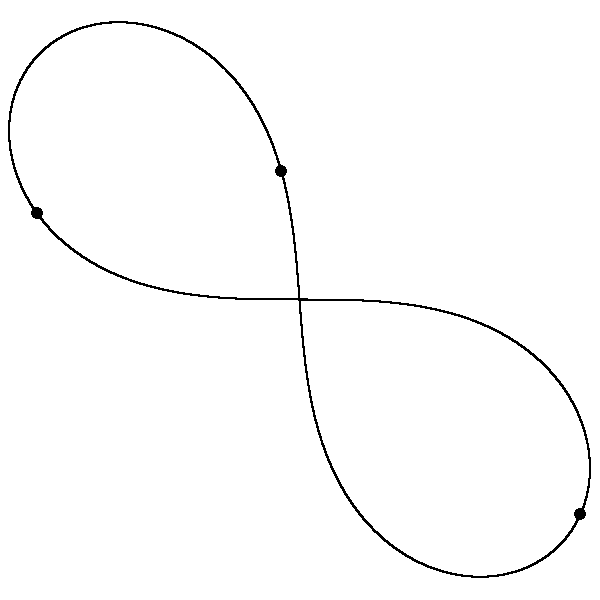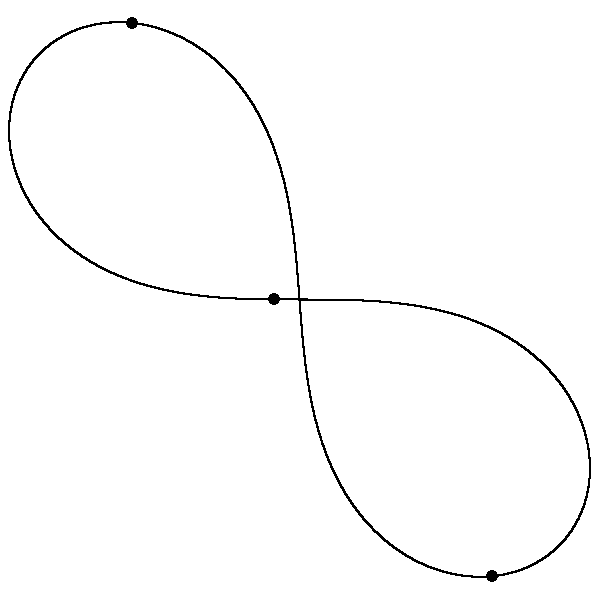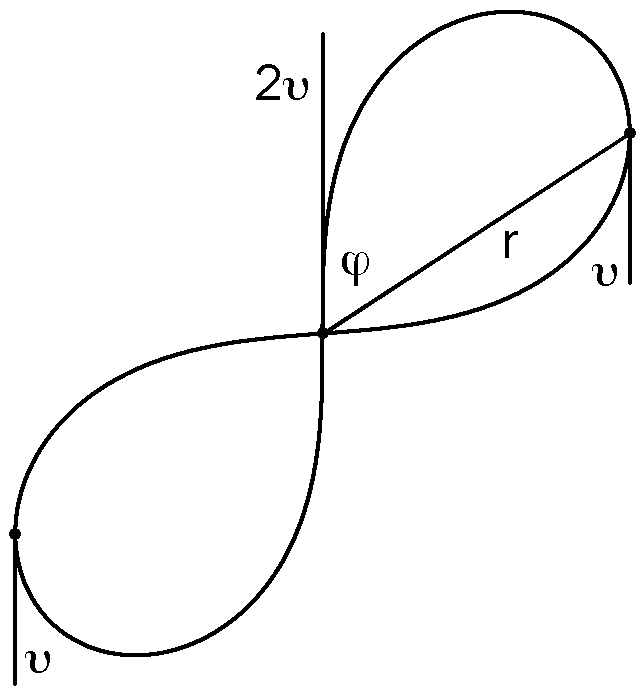Achter-Bahn
Drei gleiche Punktmassen können sich unter dem alleinigen Einfluss der gegenseitigen Gravitation auf einer Bahn in Form einer Acht bewegen. (Es ist keine Bernoulli-Lemniskate.) Die Startwerte wurden durch numerische Optimierung gesucht. Eine Simulation in BASIC produzierte 40 Einzelbilder, die ich zu einem animated gif zusammensetzte.
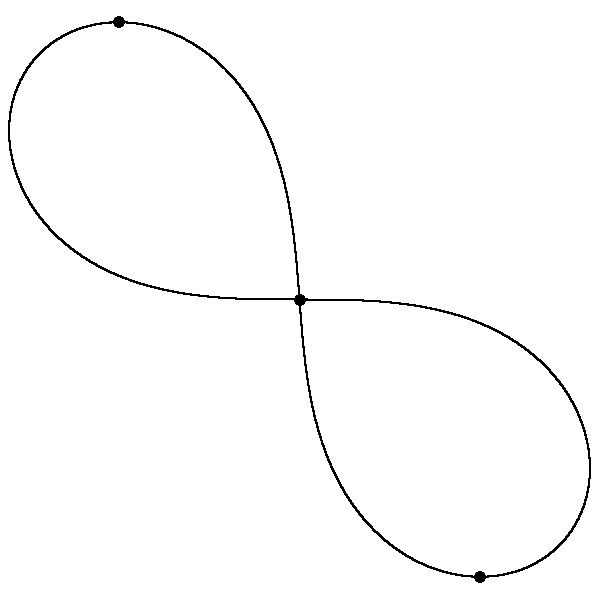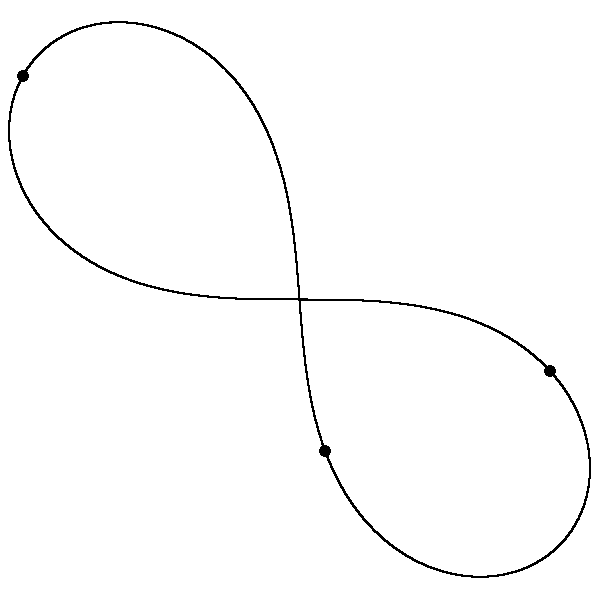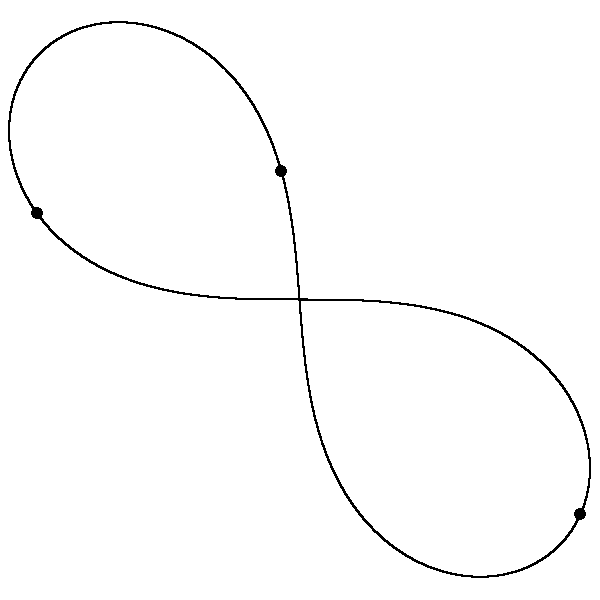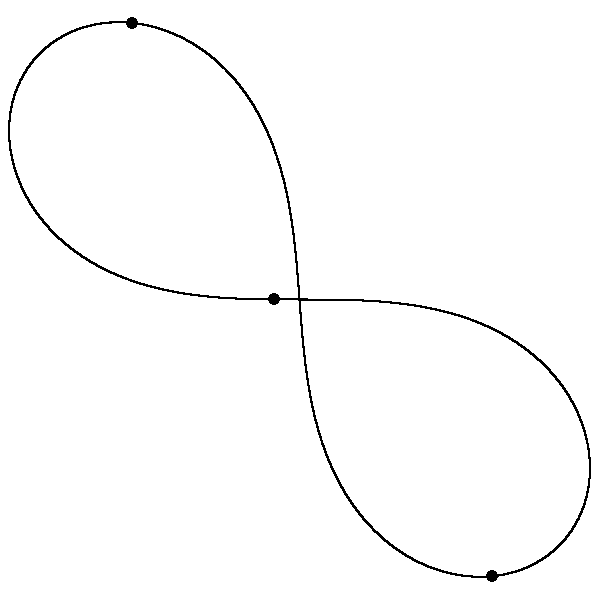
Diese Lösung des Dreikörperproblems wurde 1993 von Cristopher Moore entdeckt und in Phys. Rev. Lett. publiziert. Die Bahn scheint sogar eine gewisse Stabilität aufzuweisen. Auf C. Moore's Homepage finden sich noch mehr Animationen: http://www.santafe.edu/~moore/gallery.html. Gedruckte Bilder findet man auch im Spektrum der Wissenschaft, Januar 2006, Seiten 98-99.
Für diejenigen, welche die Bahn selber simulieren wollen, folgen hier die notwendigen Angaben:
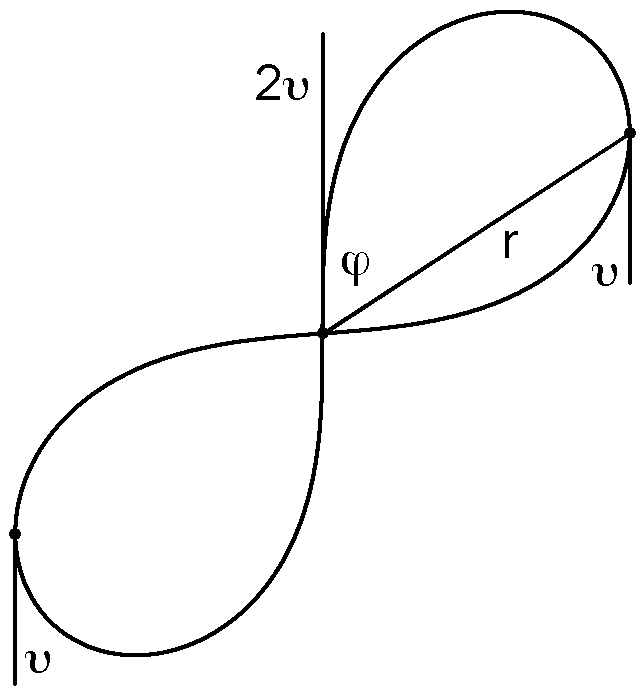
Abbildung: Für diese Startposition gilt φ = 0.993311 rad und Epot:Ekin = -2.061259 (4 bis 5 Stellen sind signifikant). In der Startposition ist Epot = -5Gm2/(2r) und Ekin = 3mv2. Alle Punktmassen m befinden sich auf derselben Geraden, der Abstand zur mittleren Masse ist r. Die zwei äusseren Massen haben Schnelligkeit v, die mittlere 2v (so wird der Gesamtimpuls Null).
erste Version: 24. September 2006, letzte Änderung: 29. Juli 2008 / M. Lieberherr