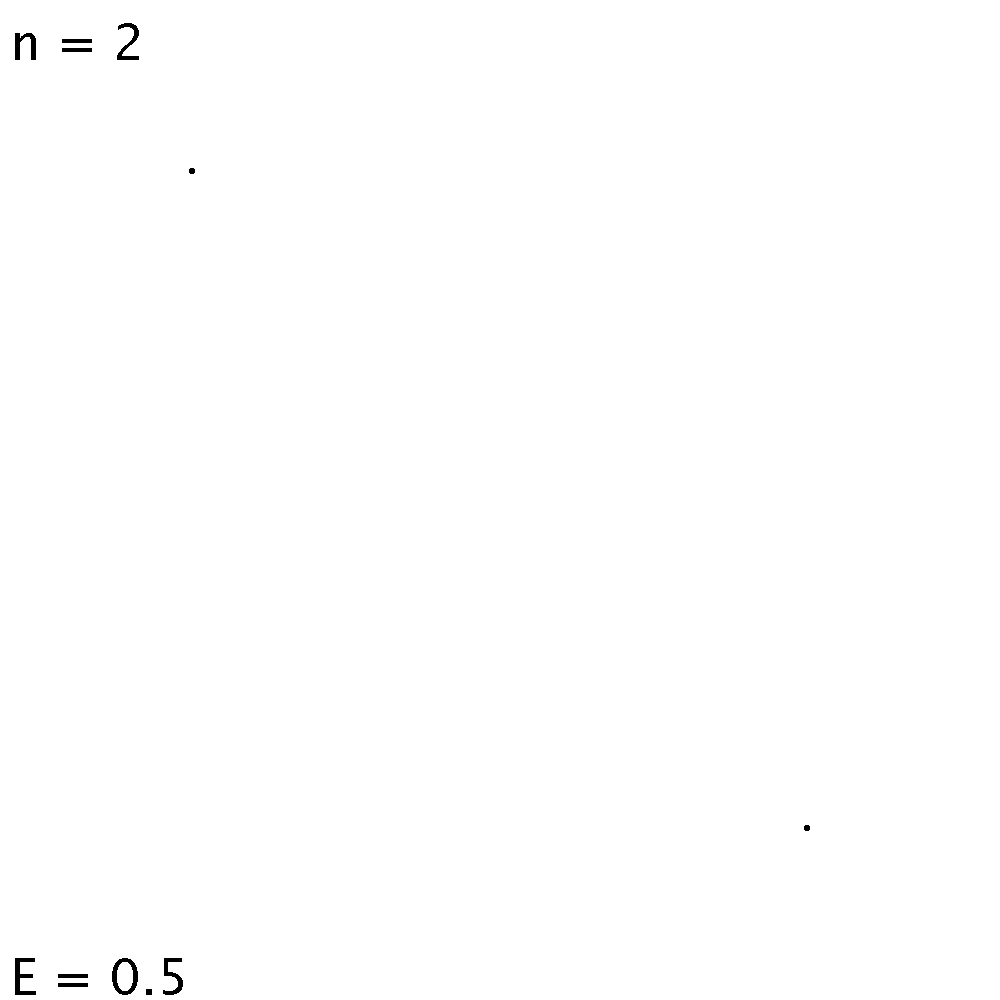
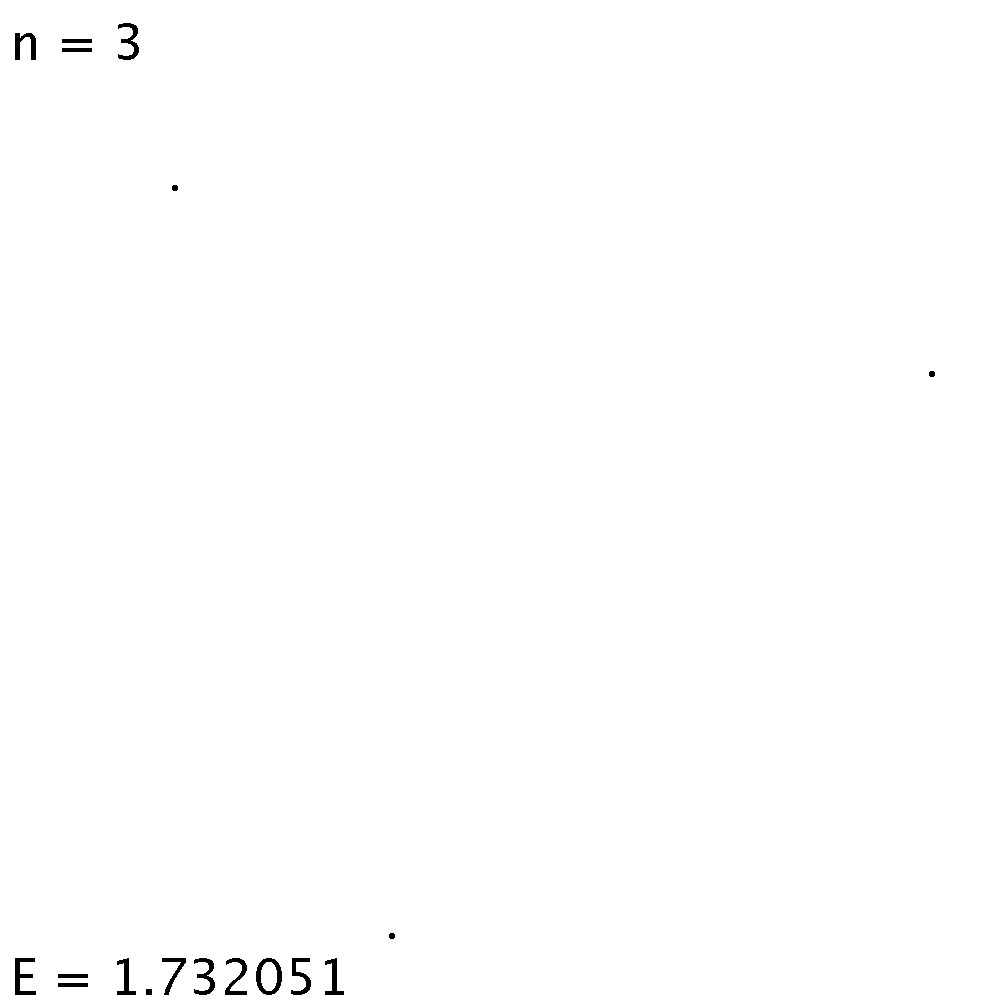
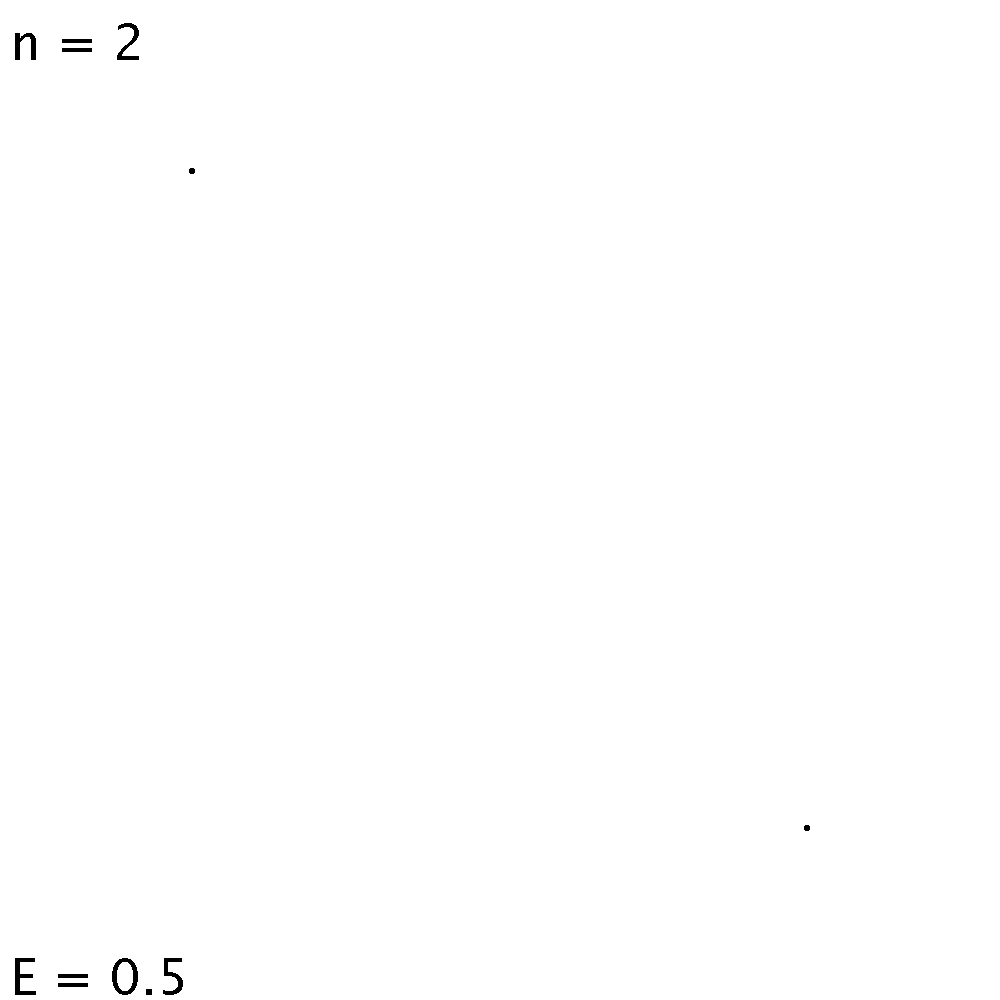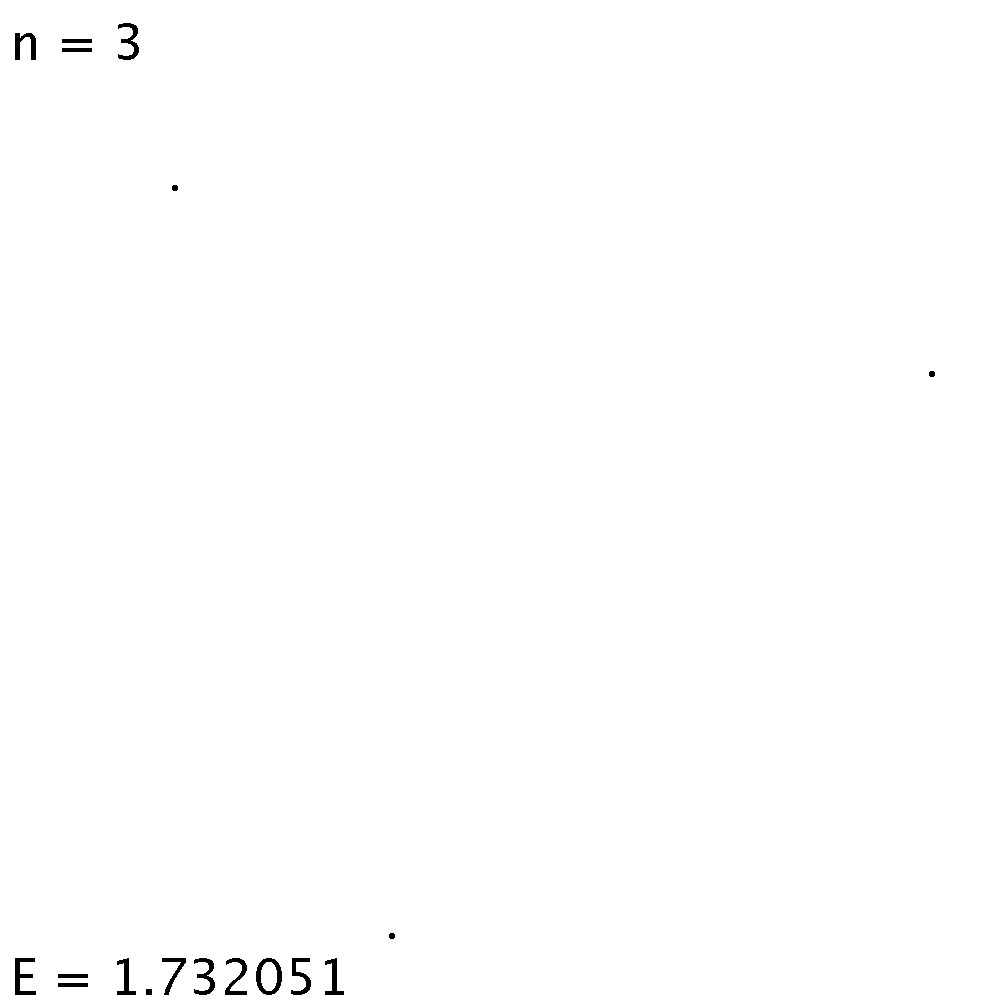Plattenladung

Wie ordnen sich n gleiche Punktladungen auf einer Kreisscheibe an, wenn sich die Ladungen unter dem Einfluss der Coulombkraft frei bewegen dürfen?

Die folgenden, simulierten Gleichgewichtszustände gingen von zufällig-gleichmässig verteilten Punktladungen auf der Kreisscheibe aus. Dann wurden die wechselseitigen Coulombkräfte sowie die potenziellen elektrostatischen Energien berechnet und aufaddiert. Dann wurde in Richtung der jeweiligen Kraft ein Schritt gemacht. Wenn die Energie in der neuen Lage tiefer war, wurde die Schrittweite leicht vergrössert, andernfalls verkleinert. Wenn eine Punktladung den Kreisrand überschritt, so wurde die radiale Komponente der Kraft eliminiert und der Abstand vom Kreiszentrum auf den Kreisradius zurückgesetzt. Für kleine n konvergierte die Simulation schnell gegen die Gleichgewichtslage, für grosse n bewegte sich die Simulation rasch in die Nähe eines Gleichgewichts, so dass von Auge keine Bewegung mehr sichtbar war, aber die Energie nahm in den hinteren Stellen weiter ab.

In den gewählten Masseinheiten ist die Kraft zwischen zwei Punktladungen F = r^-2 und die Energie E = r^-1. Die Kreisscheibe wurde durch einen Einheitskreis begrenzt.

In den folgenden Bildern ist oben links die Zahl n der Punktladungen angegeben und unten links die potenzielle Energie dieser Anordnung (die Summe der inversen Abstände aller Ladungen in den gewählten Einheiten). Die Bilder sind 1000x1000 Pixel grosse, schwarz-weisse gif-Dateien.


Zwei Punktladungen liegen im Gleichgewicht auf zwei gegenüber liegenden Enden eines Durchmessers. Weil der Durchmesser des Einheitskreises Länge 2 hat, ist die Energie 1/2.	Im Gleichgewicht liegen drei Punktladungen auf den Ecken eines gleichseitigen Dreiecks. Eine Seite hat Länge √3. Drei Mal der Kehrwert davon gibt die Energie.


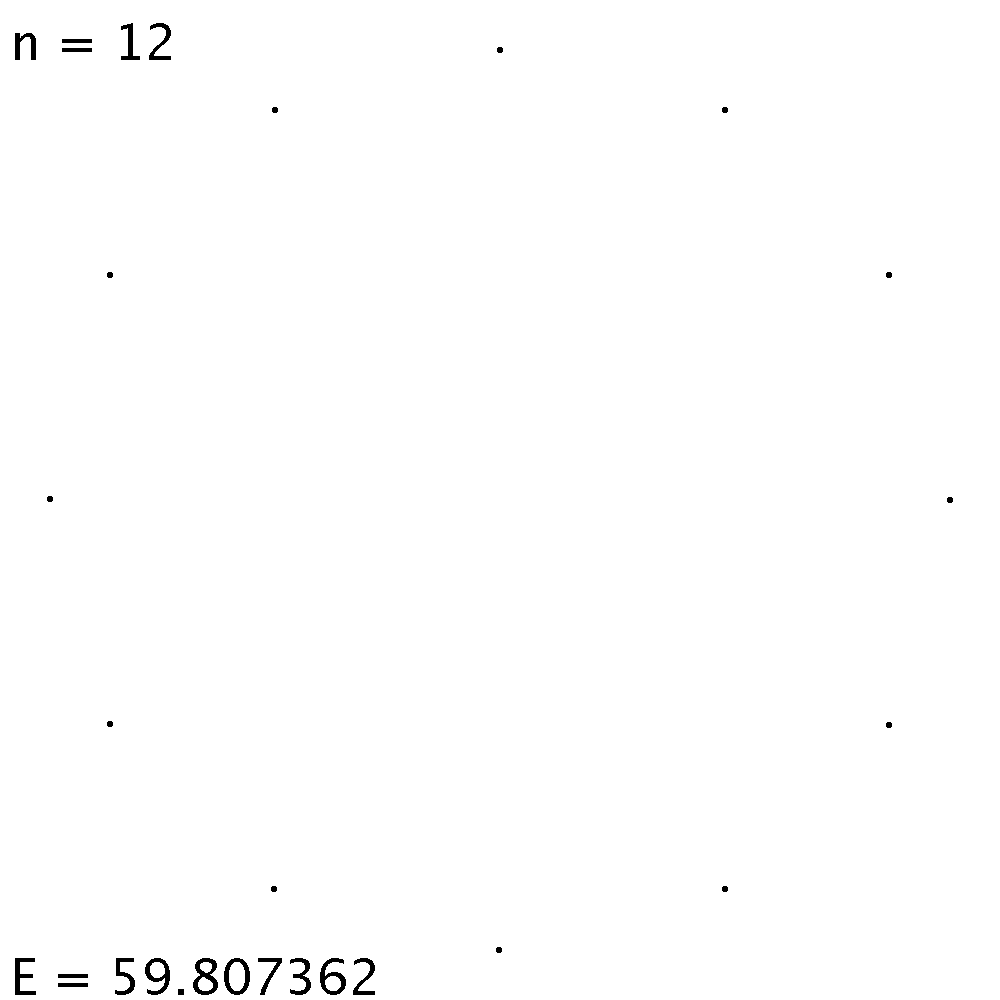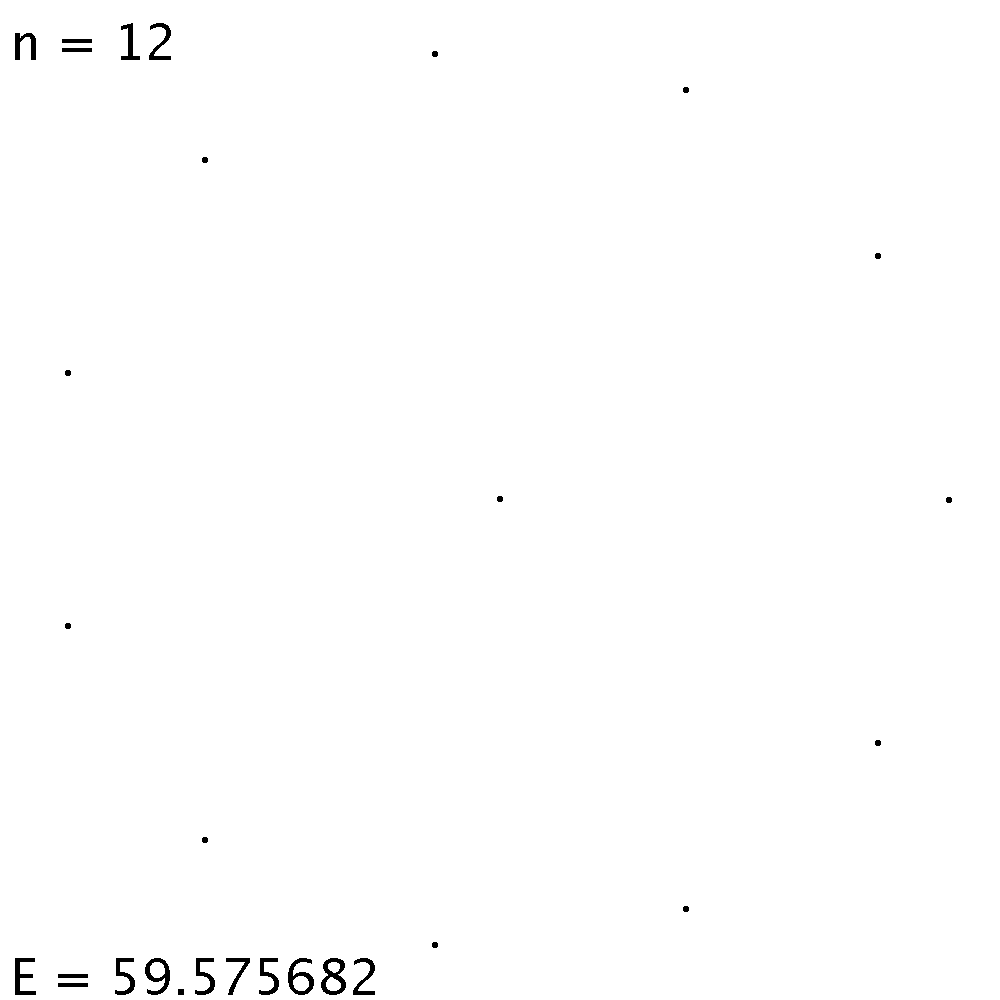Bis n = 11 liegen die Ladungen auf den Ecken eines regulären Polygons.	Ab n = 12 Punktladungen ist die regelmässige Anordnung auf dem Rand zwar eine Gleichgewichtslage, aber ...	.. die elektrostatische Energie ist tiefer, wenn man eine Ladung ins Zentrum setzt.



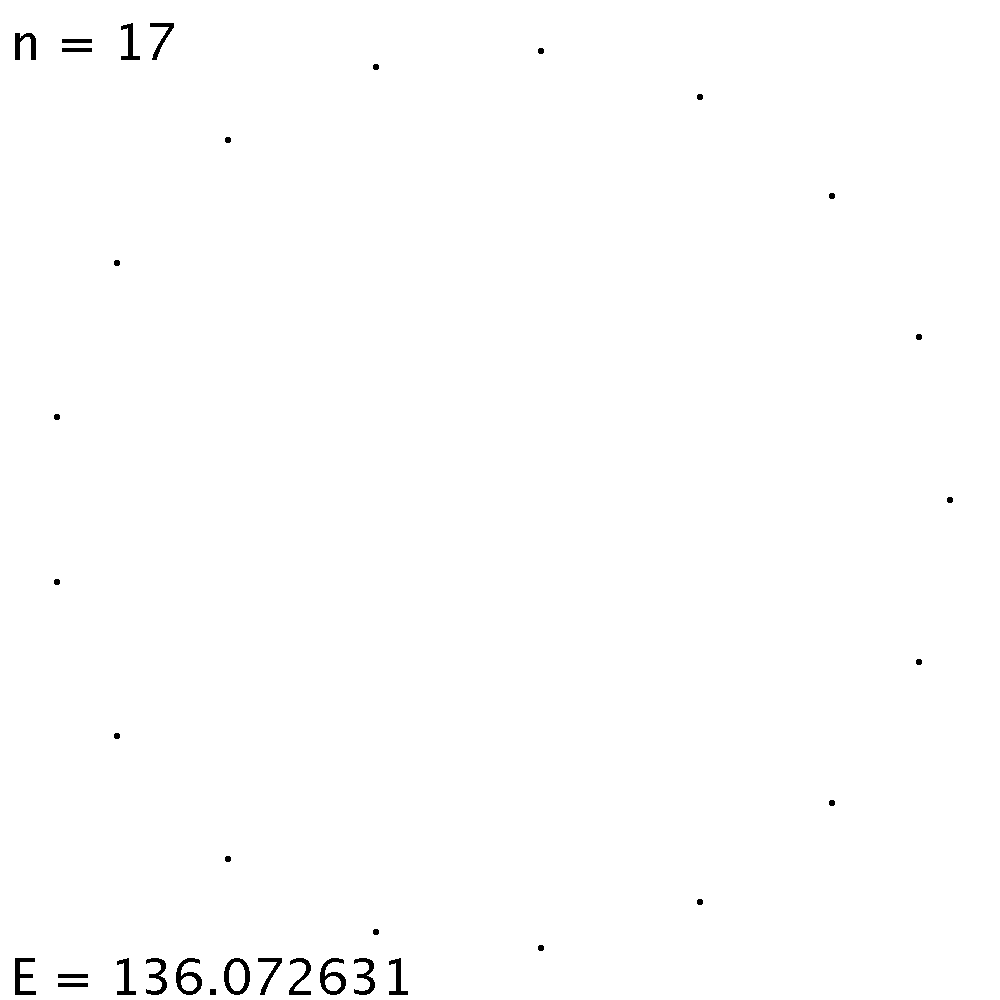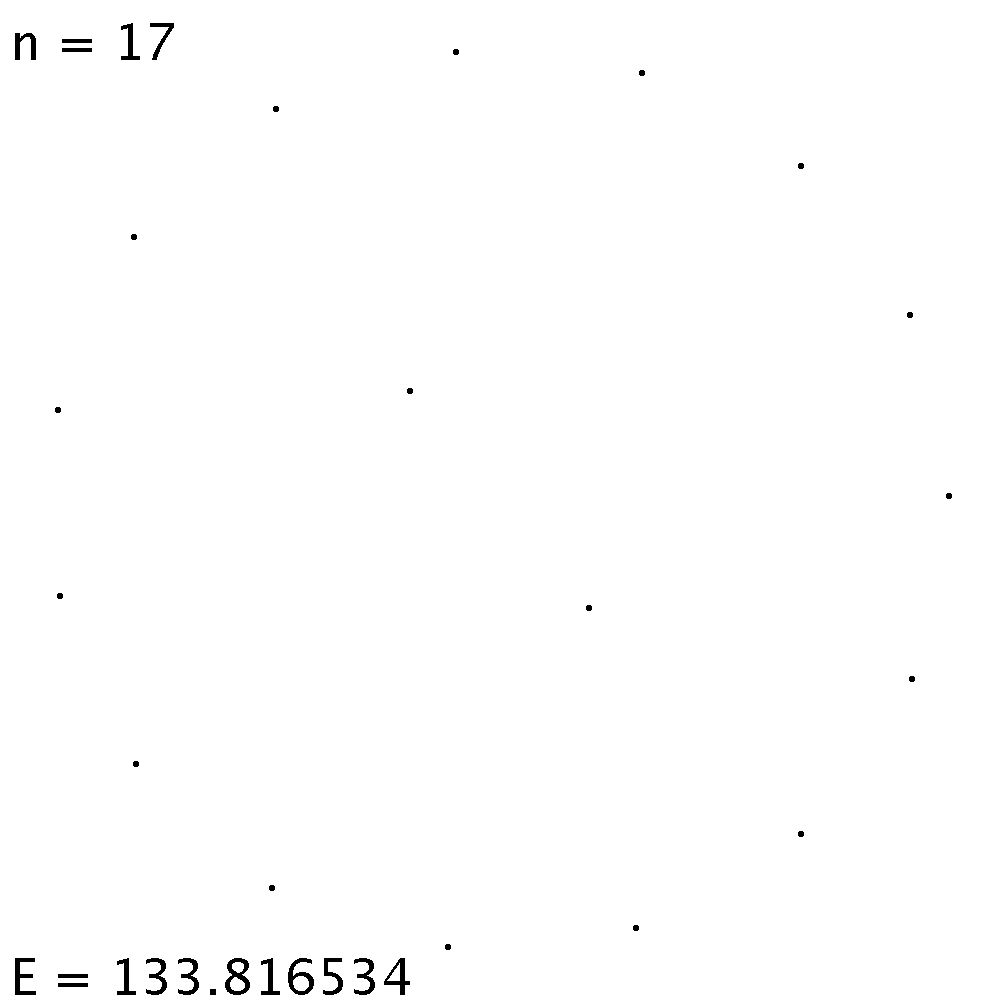Ab n = 17 ist jene Gleichgewichtslage, welche 2 Ladungen im Innern und 15 am Rand hat, energetisch am tiefsten.


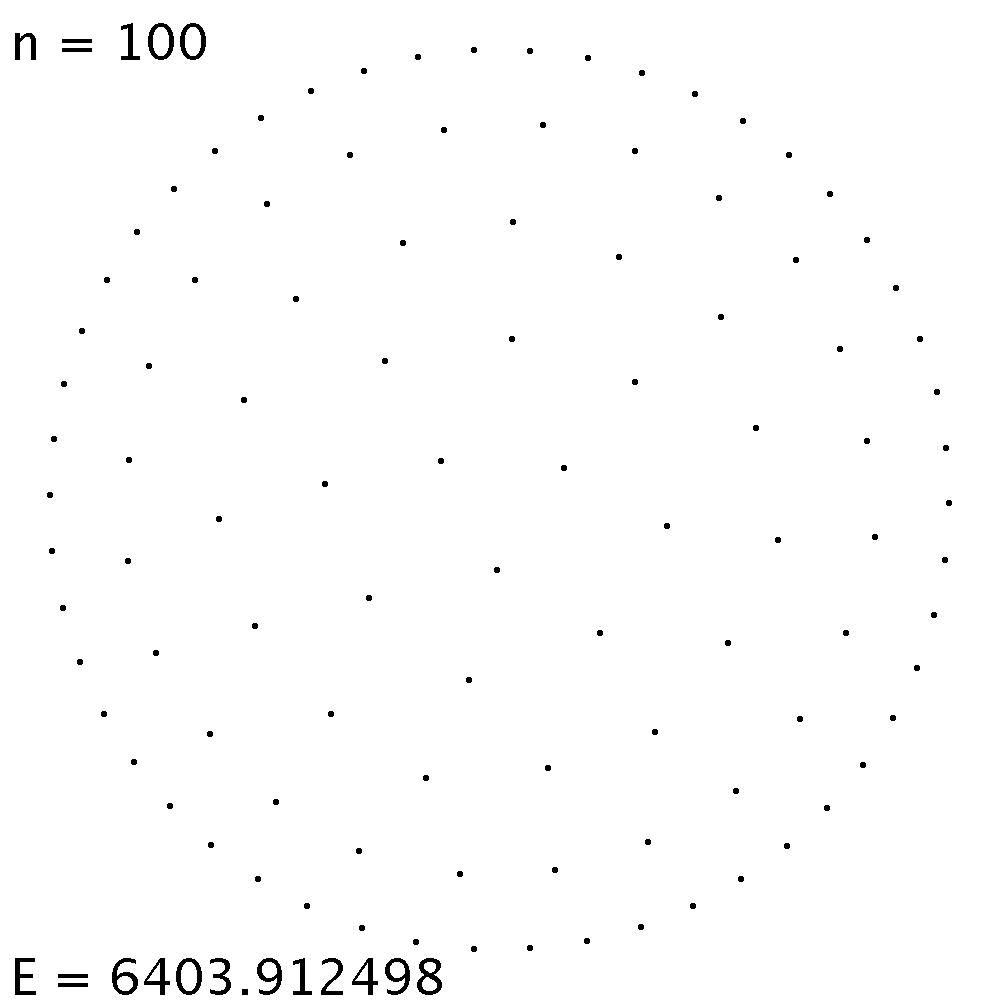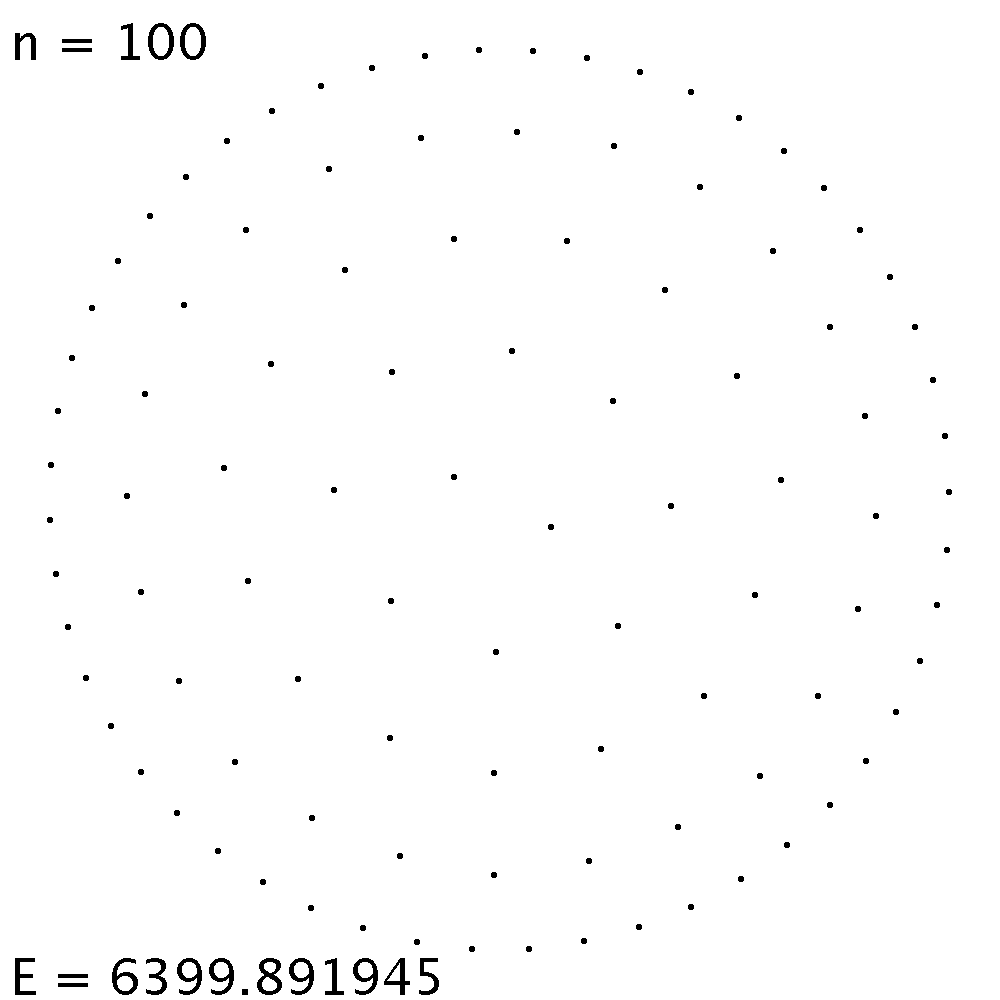
Die linke Gleichgewichtslage ist energetisch etwas günstiger als die rechte. Die Unterschiede in der elektrostatischen Energie sind allerdings gering. Die Ladungen ordnen sich ungefähr auf konzentrischen Kreisen an.	Startet die Simulation aus einer zufälligen Verteilung, so endet sie fast sicher in einem Gleichgewicht, das ein energetisches Nebenminimum darstellt.


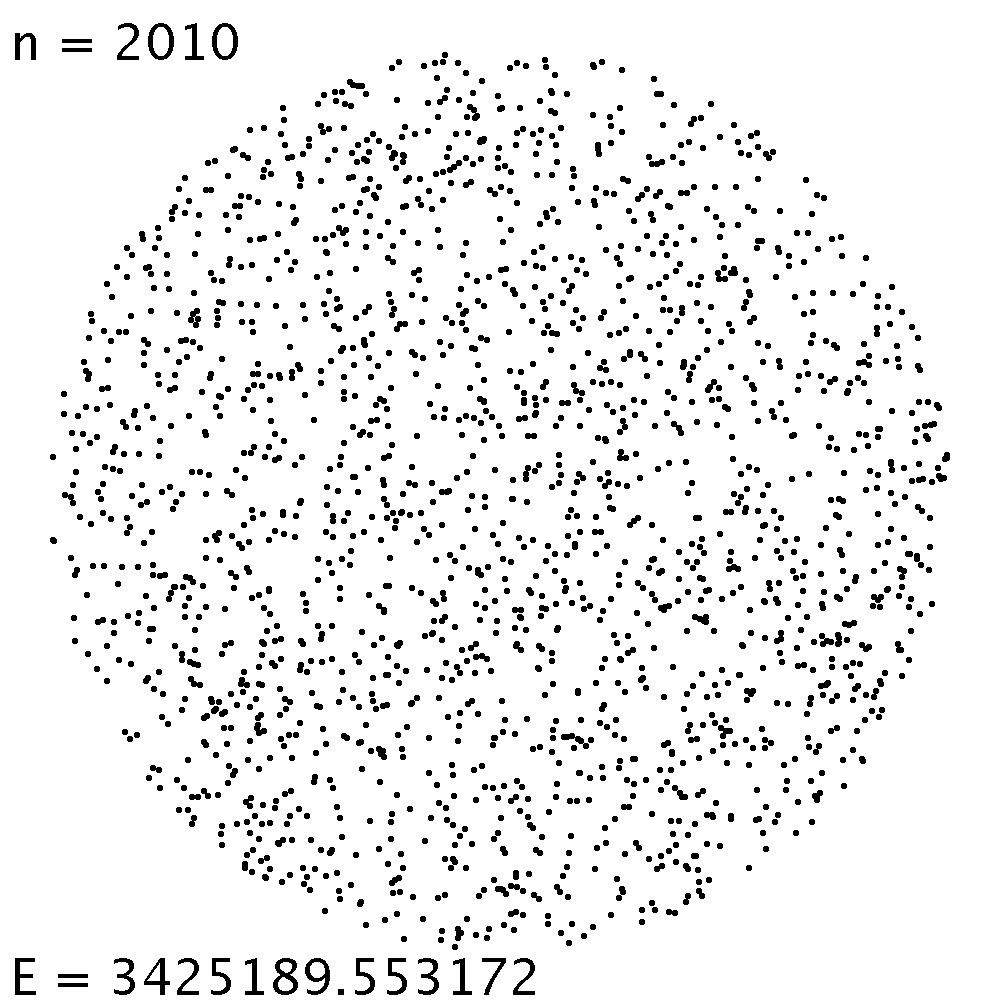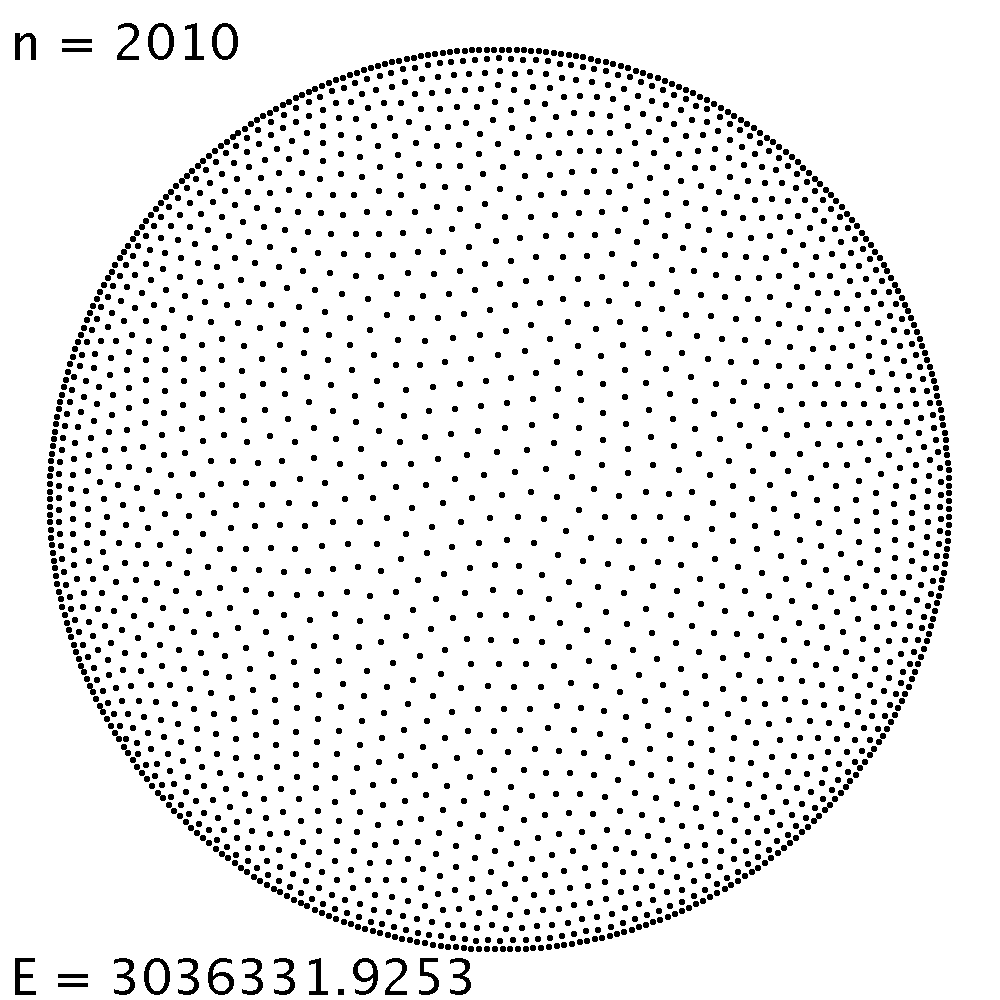
Bei sehr vielen Punktladungen kann man von Auge sehen, dass die Gleichgewichtsverteilung ungleichmässig ist, nämlich erhöht gegen den Kreisrand hin. E/n² = 0.752	Aber auch hier ist die Energie der Gleichgewichtslage nur wenig tiefer als die Energie der zufälligen Anfangsverteilung. E/n² = 0.848

Denkt man sich die Ladung als Kontinuum, so kann die Flächenladungsdichte σ der Gleichgewichtsverteilung exakt berechnet werden (als Spezialfall eines geladenen Ellipsoids):
σ(r) = Q (2πR)^-1 (R²-r²)^-1/2 mit Kreisradius R.
(nach M. G. Calkin, D. Kiang, and D. A. Tindall, "Minimum-energy charge configurations," Am. J. Phys. 55 (2), 157-158 (1987) )
Im Fall der kontinuierlich gedachten Ladung lässt sich die Kapazität einer freistehenden Kreisscheibe aus der Kapazität des Ellipsoids herleiten. Man erhält C = 8εR (wikipedia, SI-Einheiten!). Somit kann auch die Energie der geladenen Scheibe berechnet werden: E = Q²/(2C).

Für sehr viele Punktladungen sollte die Simulation gegen den kontinuierlichen Fall konvergieren. Man kann in den Abbildungen tatsächlich sehen, dass sich die Punktladungen am Kreisrand konzentrieren; im kontinuierlichen Fall divergiert dort die Flächenladungsdichte. Auch die Energie zeigt das gewünschte Verhalten: Mit Q = n·q folgt aus der Theorie E/n² = π/4 = 0.7854 in den gewählten Einheiten. Die statistisch homogene Ladungsverteilung auf der Kreisscheibe liefert in einer Simulation (bis n ≈ 20'000) den Zusammenhang E/n² ≈ 0.848.

30. Juli 2010 / Martin Lieberherr

Zum Seitenanfang